Question

在平面直角坐标系中，△AOC中，∠ACO=90°．把AO绕O点顺时针旋转90°得OB，连接AB，作BD⊥直线CO于D，点A的坐标为（-3，1）．
（1）求直线AB的解析式；
（2）若AB中点为M，连接CM，动点P、Q分别从C点出发，点P沿射线CM以每秒

2

个单位长度的速度运动，点Q沿线段CD以每秒1个长度的速度向终点D运动，当Q点运动到D点时，P、Q同时停止，设△PQO的面积为S（S≠0），运动时间为T秒，求S与T的函数关系式，并直接写出自变量T的取值范围；
（3）在（2）的条件下，动点P在运动过程中，是否存在P点，使四边形以P、O、B、N（N为平面上一点）为顶点的矩形？若存在，求出T的值．

Answer 1

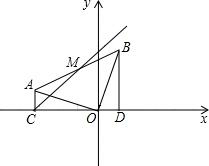
分析：（1）先求出点B的坐标，再代入一次函数的解析式即可；
（2）根据AB中点为M，求出点M的坐标，再求出CM的解析式，过点P做PH⊥CO交CO于点H，用t表示出OQ和PH的长，根据S=

1

2

OQ•PH即可求出S与T的函数关系式；
（3）此题需分四种情况分别求出T的值即可．

解答：解：（1）∵∠AOB=90°，
∴∠AOC+∠BOD=90°
∵∠BDO=90°，
∠OBD+∠BOD=90°，
∠AOC=∠BOD，
∵OA=OB，∠ACO=∠BDO=90°，
∴△AOC≌△OBD，
∴AC=OD，CO=BD
∵A（-3，1），
∴AC=OC=1，OC=BD=3，
∴B（1，3），
∴y=

1

2

x+

5

2

；

（2）M（-1，2），C（-3，0），
∴直线MC的解析式为：y=x+3
∴∠MCO=45°，
过点P做PH⊥CO交CO于点H，
S=

1

2

OQ•PH=

1

2

（3-t）×t=-

1

2

t²+

3

2

t（0＜t＜3）
或S=

1

2

（t-3）t=

1

2

t²-

3

2

t（3＜t≤4）；

（3）①当OP⊥OB时，t₁=

3

4

，t₃=

13

4

，
②当∠OPB=90°时，t₂=3，t₄=2．

点评：此题考查了一次函数的综合应用，解题时要注意分类讨论，关键是能用t表示出线段的长度求出解析式．