题目内容
（x+y+2）（x+y+3）=6，求x+y．
分析：先设x+y=z，故原式可化为（z+2）（z+3）=6，求出z的值即可．
解答：解：设x+y=z，则原式可化为（z+2）（z+3）=6，即z2+5z=0，
提取公因式得，z（z+5）=0，解得z1=0，z2=-5，即x+y=0或x+y=-5．
提取公因式得，z（z+5）=0，解得z1=0，z2=-5，即x+y=0或x+y=-5．
点评：本题考查的是用因式分解法解一元二次方程，先把x+y当作一个整体求解是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC为等边三角形，∠1=∠2=∠3．
如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为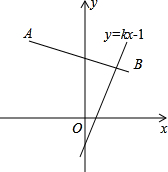
如图，在平面直角坐标系中，线段AB的端点坐标为A（-3，5）、B（2，3），如果直线y=kx-1与线段AB有交点，则k的值不可能是（ ）
某公园一块草坪的形状如图所示，用代数式表示它的面积．