题目内容
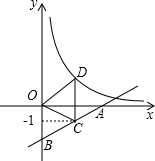 (2012•包头)如图,直线y=
(2012•包头)如图,直线y=| 1 |
| 2 |
| k |
| x |
| 5 |
| 2 |
3
3
.分析:把x=2代入y=
x-2求出C的纵坐标,得出OM=2,CM=1,根据CD∥y轴得出D的横坐标是2,根据三角形的面积求出CD的值,求出MD,得出D的纵坐标,把D的坐标代入反比例函数的解析式求出k即可.
| 1 |
| 2 |
解答:解:∵点C在直线AB上,即在直线y=
x-2上,点C的纵坐标为-1,
∴代入得:-1=
x-2,
解得,x=2,即C(2,-1),
∴OM=2,
∵CD∥y轴,S△OCD=
,
∴
CD×OM=
,
∴CD=
,
∴MD=
-1=
,
即D的坐标是(2,
),
∵D在双曲线y=
上,
∴代入得:k=2×
=3.
故答案为:3.
| 1 |
| 2 |

∴代入得:-1=
| 1 |
| 2 |
解得,x=2,即C(2,-1),
∴OM=2,
∵CD∥y轴,S△OCD=
| 5 |
| 2 |
∴
| 1 |
| 2 |
| 5 |
| 2 |
∴CD=
| 5 |
| 2 |
∴MD=
| 5 |
| 2 |
| 3 |
| 2 |
即D的坐标是(2,
| 3 |
| 2 |
∵D在双曲线y=
| k |
| x |
∴代入得:k=2×
| 3 |
| 2 |
故答案为:3.
点评:本题考查了反比例函数与一次函数的交点问题、一次函数、反比例函数的图象上点的坐标特征、三角形的面积等知识点,通过做此题培养了学生的计算能力和理解能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
 坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.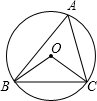 (2012•包头)如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,则BC的长为
(2012•包头)如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,则BC的长为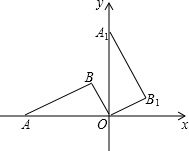 (2012•包头)如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(-1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为
(2012•包头)如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(-1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为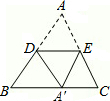 (2012•包头)如图,将△ABC纸片的一角沿DE向下翻折,使点A落在BC边上的A′点处,且DE∥BC,下列结论:
(2012•包头)如图,将△ABC纸片的一角沿DE向下翻折,使点A落在BC边上的A′点处,且DE∥BC,下列结论: