题目内容
把抛物线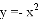 向右平移
向右平移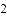
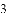
A. y=-(x+2) 2+3 B. y=-(x-2) 2+3 C. y=-(x+2) 2-3 D. y=-(x-2) 2-3
练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
题目内容
把抛物线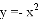 向右平移
向右平移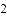
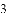
A. y=-(x+2) 2+3 B. y=-(x-2) 2+3 C. y=-(x+2) 2-3 D. y=-(x-2) 2-3
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案