题目内容
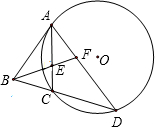 如图,已知等腰△ABC,AB=AC,过A、C两点的圆⊙O切AB于A,BC的延长线交⊙O于D,∠ABD的角平分线交AC于E,交AD于F.
如图,已知等腰△ABC,AB=AC,过A、C两点的圆⊙O切AB于A,BC的延长线交⊙O于D,∠ABD的角平分线交AC于E,交AD于F.
(1)求证:AE=AF;(2)若AC=CD=2,求AD.
(1)证明:∵BF平分∠ABD,
∴∠AEF=∠BAC+ ∠ABC,∠AFE=∠ADB+
∠ABC,∠AFE=∠ADB+ ∠ABC,
∠ABC,
又∵∠BAC=∠ADB,
∴AE=AF;
(2)解:∵AB是⊙O切线,AC=CD=2,
∴AB2=BC•BD
∴4=BC×(BC+2)
∴BC= -1,BC=-
-1,BC=- -1(舍去),
-1(舍去),
∵AC=CD=2,
∴∠CAD=∠D,
∵AB是⊙O切线,
∴∠BAC=∠D,
∴AC是∠BAD的平分线,
∴ =
=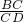 ,
,
∴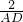 =
=
∴AD=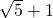 .
.
答;AD的长为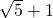 .
.
分析:(1)根据弦切角定理可知∠BAC=∠ADB,由∠ABD的角平分线交AC于E,交AD于F,可得∠AEF=∠BAC+ ∠ABC,∠AFE=∠ADB+
∠ABC,∠AFE=∠ADB+ ∠ABC,问题得证;
∠ABC,问题得证;
(2)根据AC=CD=2,利用切割线定理求出BC,再求证AC是∠BAD的平分线,然后可得 =
=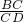 即可得出答案,
即可得出答案,
点评:此题主要考查学生对切割线定理、弦切角定理的理解和掌握,解答(2)的关键是利用切割线定理求出BC,然后再利用角平分线的性质即可求出AD.
∴∠AEF=∠BAC+
 ∠ABC,∠AFE=∠ADB+
∠ABC,∠AFE=∠ADB+ ∠ABC,
∠ABC,又∵∠BAC=∠ADB,
∴AE=AF;
(2)解:∵AB是⊙O切线,AC=CD=2,
∴AB2=BC•BD
∴4=BC×(BC+2)
∴BC=
 -1,BC=-
-1,BC=- -1(舍去),
-1(舍去),∵AC=CD=2,
∴∠CAD=∠D,
∵AB是⊙O切线,
∴∠BAC=∠D,
∴AC是∠BAD的平分线,
∴
 =
=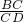 ,
,∴
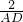 =
=
∴AD=
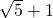 .
.答;AD的长为
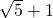 .
.分析:(1)根据弦切角定理可知∠BAC=∠ADB,由∠ABD的角平分线交AC于E,交AD于F,可得∠AEF=∠BAC+
 ∠ABC,∠AFE=∠ADB+
∠ABC,∠AFE=∠ADB+ ∠ABC,问题得证;
∠ABC,问题得证;(2)根据AC=CD=2,利用切割线定理求出BC,再求证AC是∠BAD的平分线,然后可得
 =
=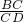 即可得出答案,
即可得出答案,点评:此题主要考查学生对切割线定理、弦切角定理的理解和掌握,解答(2)的关键是利用切割线定理求出BC,然后再利用角平分线的性质即可求出AD.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
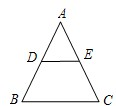 如图,已知等腰△ABC的面积为8cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面积为
如图,已知等腰△ABC的面积为8cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面积为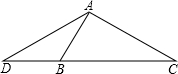 如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB.
如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB. (2010•西藏)如图,已知等腰△ABC,AC=BC=10,AB=12,以BC为直径作⊙O交AB点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(2010•西藏)如图,已知等腰△ABC,AC=BC=10,AB=12,以BC为直径作⊙O交AB点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E. 如图,已知等腰△ABC中,AB=AC,P、Q分别为AC、AB上的点,且AP=PQ=QB=BC,则∠PCQ的度数为( )
如图,已知等腰△ABC中,AB=AC,P、Q分别为AC、AB上的点,且AP=PQ=QB=BC,则∠PCQ的度数为( ) 如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,
如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,