题目内容
已知凸四边形ABCD的四边长为AB=8，BC=
，CD=DA=6，∠D=90°，则四边形ABCD的面积为________．
18+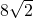
分析：根据直角△ADC中AD，CD求AC，并计算△ADC的面积，根据AC，AB，BC的长判断△ABC为直角三角形，根据直角△的面积公式求△ACB的面积，四边形ABCD的面积为△ABC和△ADC的面积和．
解答：在△ADC中，∠D=90°，
∴△ADC的面积为
×AD×DC=18，
且AC2=AD2+DC2=36+36=72
AB2+BC2=64+8=72
即AB2+BC2=AC2，∴△ABC是直角三角形
∴△ABC的面积为×AB×BC=8
，
故四边形ABCD面积为△ADC的面积和△ABC的面积之和为18+8．
故答案为 18+8．
点评：本题考查了勾股定理的运用，考查了勾股定理逆定理的运用，本题中根据AB2+BC2=AC2判定△ABC是直角三角形是解题的关键．
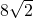
分析：根据直角△ADC中AD，CD求AC，并计算△ADC的面积，根据AC，AB，BC的长判断△ABC为直角三角形，根据直角△的面积公式求△ACB的面积，四边形ABCD的面积为△ABC和△ADC的面积和．
解答：在△ADC中，∠D=90°，
∴△ADC的面积为
×AD×DC=18，且AC2=AD2+DC2=36+36=72
AB2+BC2=64+8=72
即AB2+BC2=AC2，∴△ABC是直角三角形
∴△ABC的面积为
×AB×BC=8，故四边形ABCD面积为△ADC的面积和△ABC的面积之和为18+8
．故答案为 18+8
．点评：本题考查了勾股定理的运用，考查了勾股定理逆定理的运用，本题中根据AB2+BC2=AC2判定△ABC是直角三角形是解题的关键．
练习册系列答案
相关题目
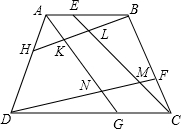如图，已知凸四边形ABCD，E，F，G，H分别在AB，BC，CD，DA上，且BE=2AE，BF=2CF，DH=2AH，DG=2CG，求证：SKLMN=S△AKH+S△BEL+S△CFM+S△DNG．
四块，然后再拼成一个平行四边形？