题目内容
随着“六一”临近,儿童礼品开始热销,某厂每月固定生产甲、乙两种礼品共100万件,甲礼品每件成本15元,乙礼品每件成本12元,现甲礼品每件售价22元,乙礼品每件售价18元,且都能全部售出。
(1)若某月销售收入2000万元,则该月甲、乙礼品的产量分别是多少?
(2)如果每月投入的总成本不超过1380万元,应怎样安排甲、乙礼品的产量,可使所获得的利润最大?
(3)该厂在销售中发现:甲礼品售价每提高1元,销量会减少4万件,乙礼品售价不变,不管多少产量都能卖出。在(2)的条件下,为了获得更大的利润,该厂决定提高甲礼品的售价,并重新调整甲、乙礼品的生产数量,问:提高甲礼品的售价多少元时可获得最大利润,最大利润为多少万元?
【答案】
(1)50万件,50万件;(2)甲礼品60万件,乙礼品40万件;(3)7元,856万元
【解析】
试题分析:(1)设生产甲礼品 万件,乙礼品
万件,乙礼品 万件,根据“月销售收入2000万元”即可列方程求解;
万件,根据“月销售收入2000万元”即可列方程求解;
(2)设生产甲礼品 万件,乙礼品
万件,乙礼品 万件,所获得的利润为
万件,所获得的利润为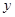 万元,根据“每月投入的总成本不超过1380万元”即可列不等式求解;
万元,根据“每月投入的总成本不超过1380万元”即可列不等式求解;
(3)设提价甲礼品 元,先根据题意列出y关于a的函数关系式,再根据二次函数的性质求解即可.
元,先根据题意列出y关于a的函数关系式,再根据二次函数的性质求解即可.
(1)设生产甲礼品 万件,乙礼品
万件,乙礼品 万件,由题意得:
万件,由题意得:
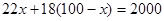
解得: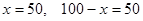
答:甲、乙礼品的产量分别是50万件,50万件;
(2)设生产甲礼品 万件,乙礼品
万件,乙礼品 万件,所获得的利润为
万件,所获得的利润为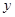 万元,由题意得
万元,由题意得
 ,解得
,解得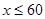
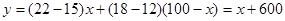
∵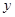 随
随 增大而增大,
增大而增大,
∴当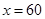 万件时,y有最大值660万元。
万件时,y有最大值660万元。
答:这时应生产甲礼品60万件,乙礼品40万件;
(3)设提价甲礼品 元,由题意得
元,由题意得
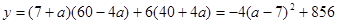
∴当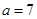 即提价甲礼品7元时,可获得最大利润856万元。
即提价甲礼品7元时,可获得最大利润856万元。
考点:二次函数的应用
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目