题目内容
 如图,AB、CD两教学楼相距30米,某学生在教室窗口B处测得CD楼楼顶C处的仰角为30°,楼底D处的俯角为45°,则CD的高度为
如图,AB、CD两教学楼相距30米,某学生在教室窗口B处测得CD楼楼顶C处的仰角为30°,楼底D处的俯角为45°,则CD的高度为
- A.(10
 +30)米
+30)米 - B.(30-
 )米
)米 - C.45米
- D.5米
A
分析:作BE⊥CD,根据俯仰角的正切值求得AB、CE的长,则CD的高度即可求出.
解答: 解:如图.作BE⊥CD.
解:如图.作BE⊥CD.
由题意得:∠CBE=30°,∠ABD=45°,
则AB= =30(米),CE=BE•tan30°=10
=30(米),CE=BE•tan30°=10 (米),
(米),
∴CD=AB+CE=10 +30 (米).
+30 (米).
故选A.
点评:本题考查俯仰角的定义,要求学生能借助俯仰角构造直角三角形并解直角三角形.
分析:作BE⊥CD,根据俯仰角的正切值求得AB、CE的长,则CD的高度即可求出.
解答:
 解:如图.作BE⊥CD.
解:如图.作BE⊥CD.由题意得:∠CBE=30°,∠ABD=45°,
则AB=
 =30(米),CE=BE•tan30°=10
=30(米),CE=BE•tan30°=10 (米),
(米),∴CD=AB+CE=10
 +30 (米).
+30 (米).故选A.
点评:本题考查俯仰角的定义,要求学生能借助俯仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目

 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB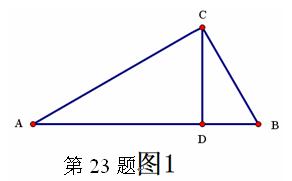
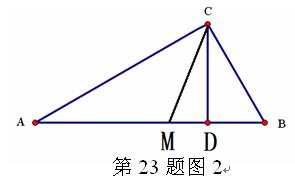
 几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB

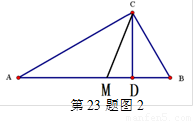 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB