题目内容
在△ABC，点D、E分别在边AB、AC上，如果AD=1，BD=2，那么由下列条件能够判定DE∥BC的是
- A.
- B.
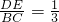
- C.
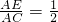
- D.
D
分析：根据相似三角形的判定得出△ADE∽△ABC即可推出∠ADE=∠B，根据平行线的判定推出即可．
解答：
∵AD=1，BD=2，
∴
=
，
只有当
=时，DE∥BC，
理由是：∵==，∠A=∠A，
∴△ADE≌△ABC，
∴∠ADE=∠B，
∴DE∥BC，
而其它选项都不能推出∠ADE=∠B或∠AED=∠C，即不能推出DE∥BC，
即选项A、B、C都错误，只有选项D正确；
故选D．
点评：本题考查了相似三角形的性质和判定，平行线的判定的应用，主要考查学生的推理能力．
分析：根据相似三角形的判定得出△ADE∽△ABC即可推出∠ADE=∠B，根据平行线的判定推出即可．
解答：
∵AD=1，BD=2，
∴
=，只有当
=时，DE∥BC，理由是：∵
==，∠A=∠A，∴△ADE≌△ABC，
∴∠ADE=∠B，
∴DE∥BC，
而其它选项都不能推出∠ADE=∠B或∠AED=∠C，即不能推出DE∥BC，
即选项A、B、C都错误，只有选项D正确；
故选D．
点评：本题考查了相似三角形的性质和判定，平行线的判定的应用，主要考查学生的推理能力．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
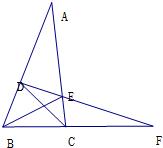20、如图，在△ABC，点D、E分别在AB、AC上，连接DE并延长交BC的延长线于点F，连接DC、BE，若∠BDE+∠BCE=180°．
