题目内容
已知二次函数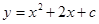
．
1.当c＝－3时，求出该二次函数的图象与x轴的交点坐标；
2.若－2＜x＜1时，该二次函数的图象与x轴有且只有一个交点，求c的取值范围．
【答案】
1.由题意，得
.
当
时，
.
解得
，
.
∴该二次函数的图象与x轴的交点坐标为（－3,0），（1，0）.
2.抛物线
的对称轴为
.
① 若抛物线与x轴只有一个交点，则交点为（－1，0）.
有
，解得
.
② 若抛物线与x轴有两个交点，且满足题意，则有
当
时，
≤0，
∴
≤0，解得
≤0.
当
时，
，
∴
，解得
.
∴
≤0.
综上所述，c的取值范围是或≤0.
【解析】
1.利用y=0计算出二次函数的图象与x轴的交步坐标；
2.分别讨论二次函数与x轴只有一交点或两个交点在－2＜x＜1只有一个交点两种情况。
练习册系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A（1，2），B（3，2），C（0，-1），D（2，3）．点P（x1，y1），Q（x2，y2）也在该函数的图象上，当0＜x1＜1，2＜x2＜3时，y1与y2的大小关系正确的是（ ）
| A、y1≥y2 | B、y1＞y2 | C、y1＜y2 | D、y1≤y2 |
（2013•莒南县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①ac＞0；②a-b+c＜0；