Question

矩形ABCD中，对角线AC、BD交于点O，AE⊥BD于E，若OE：ED=1：3，AE=，则BD=________．

Answer 1

4或
分析：由于AB为矩形的长边或短边不能确定，所以应分两种情况进行讨论：
AB是矩形较短边时可设出OE=x，ED=3x，然后在直角三角形OEA中利用勾股定理进行求解；
当AB是矩形较长边时，设OE=x，则ED=3x，在Rt△AOE中利用勾股定理可求出x的值，进而得出结论．
解答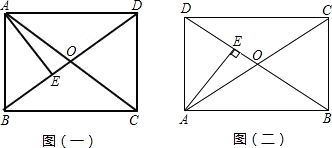：解：如图（一）所示，
AB是矩形较短边时，
∵矩形ABCD，
∴OA=OD=；
∵OE：ED=1：3，
∴可设OE=x，ED=3x，则OD=2x
∵AE⊥BD，AE=，
∴在Rt△OEA中，x²+（）²=（2x）²，
∴x=1
∴BD=4．
当AB是矩形较长边时，如图（二）所示，
∵OE：ED=1：3，
∴设OE=x，则ED=3x，
∵OA=OD，
∴OA=4x，
在Rt△AOE中，x²+（）²=（4x）²，
∴x=，
∴BD=8x=8×=．
故答案为：4或．
点评：本题的关键是设出未知数，利用勾股定理把求线段的长的问题转化为方程问题．