题目内容
抛物线y=x2-（2m-1）x-2m与x轴的两个交点为A（x1，0），B（x2，0），若|
|=1，则m的值为
- A.-
- B.±
- C.0
- D.
D
分析：本题要分两种情况来解：一、两根相等时，即△=0；二、两根互为相反数时，即2m-1=0．
解答：∵||=1，
∴x1=±x2，两根相等（不合题意舍去）或互为相反数，即2m-1=0．
2m-1=0时m=．
故选D．
点评：二次函数和一元一次方程有以下关系：方程有两个不相等的实数根，二次函数的图象与x轴有两个交点；方程有两个相等的实数根，二次函数的图象与x轴有1个交点；方程没有实数根，二次函数的图象与x轴没有交点．
分析：本题要分两种情况来解：一、两根相等时，即△=0；二、两根互为相反数时，即2m-1=0．
解答：∵|
|=1，∴x1=±x2，两根相等（不合题意舍去）或互为相反数，即2m-1=0．
2m-1=0时m=
．故选D．
点评：二次函数和一元一次方程有以下关系：方程有两个不相等的实数根，二次函数的图象与x轴有两个交点；方程有两个相等的实数根，二次函数的图象与x轴有1个交点；方程没有实数根，二次函数的图象与x轴没有交点．
练习册系列答案
阅读快车系列答案
相关题目
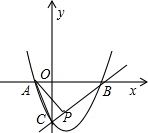A是抛物线与x轴的另一个交点．
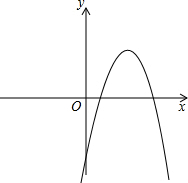已知一元二次方程-x2+bx+c=0的两个实数根是m，4，其中0＜m＜4．
16、已知抛物线y=x2+bx+c的部分图象如图所示，若方程x2+bx+c=0有两个同号的实数根，则c的值可以是