题目内容
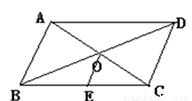
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为_____.
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
题目内容
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为_____.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案