题目内容
已知Rt△ABC和Rt△ADE,∠ACB=∠AED=90°,∠BAC=∠DAE=30°,P为线段BD的中点,连接PC,PE.
(1)如图1,若AC=AE,C、A、E依次在同一条直线上,则∠CPE= ;PC与PE存在的等量关系是 ;
(2)如图2,若AC≠AE,C、A、E依次在同一条直线上,猜想∠CPE的度数及PC与PE存在的等量关系,并写出你的结论;(不需要证明) ;
(3)如图3,在图2的基础上,若将Rt△ADE绕点A逆时针任意旋转一个角度,使C、A、E不在一条直线上,试探究∠CPE的度数及PC与PE存在的等量关系,写出你的结论并说明理由.

(1)如图1,若AC=AE,C、A、E依次在同一条直线上,则∠CPE=
(2)如图2,若AC≠AE,C、A、E依次在同一条直线上,猜想∠CPE的度数及PC与PE存在的等量关系,并写出你的结论;(不需要证明)
(3)如图3,在图2的基础上,若将Rt△ADE绕点A逆时针任意旋转一个角度,使C、A、E不在一条直线上,试探究∠CPE的度数及PC与PE存在的等量关系,写出你的结论并说明理由.

考点:四边形综合题
专题:压轴题
分析:(1)利用“角边角”证明△ABC和△ADE全等,根据全等三角形对应边相等可得BC=DE,延长CP、ED,相交于点F,根据中点定义可得BP=DP,再求出BC∥DE,然后利用两直线平行,内错角相等求出∠F=∠BCP,然后利用“角角边”证明△BCP和△DFP全等,根据全等三角形对应边相等可得CP=PF,BC=DF,然后根据直角三角形斜边上的中线等于斜边的一半可得PC=PE=PF,根据等边对等角可得∠F=∠PEF,再根据三角形的中位线定理可得∠F=∠ADE,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)延长CP、ED,相交于点F,根据中点定义可得BP=DP,再求出BC∥DE,然后利用两直线平行,内错角相等求出∠F=∠BCP,然后利用“角角边”证明△BCP和△DFP全等,根据全等三角形对应边相等可得CP=PF,BC=DF,然后根据直角三角形斜边上的中线等于斜边的一半可得PC=PE=PF,根据等边对等角可得∠F=∠PEF,再解直角三角形求出AC=
BC,AE=
DE,然后求出
=
,根据平行线分线段成比例定理求出AD∥CF,求出∠F=∠ADE,再利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(3)取AB的中点M,AD的中点N,连接CM、PM、EN、PN,利用三角形中位线定理求出PM∥AD,PN∥AB,然后求出四边形AMPN是平行四边形,根据平行四边形的对边相等和直角三角形斜边上的中线等于斜边的一半求出CM=PN,PM=NE,再求出∠PMC=∠ENP,然后利用“边角边”证明△PMC和△ENP全等,根据全等三角形对应边相等可得PC=PE,全等三角形对应角相等可得∠PCM=∠EPN,然后求出∠CPE=∠CPM+∠PCM+∠PMB,再利用三角形内角和定理列式计算即可求出∠CPE=120°.
(2)延长CP、ED,相交于点F,根据中点定义可得BP=DP,再求出BC∥DE,然后利用两直线平行,内错角相等求出∠F=∠BCP,然后利用“角角边”证明△BCP和△DFP全等,根据全等三角形对应边相等可得CP=PF,BC=DF,然后根据直角三角形斜边上的中线等于斜边的一半可得PC=PE=PF,根据等边对等角可得∠F=∠PEF,再解直角三角形求出AC=
| 3 |
| 3 |
| AE |
| AC |
| DE |
| DF |
(3)取AB的中点M,AD的中点N,连接CM、PM、EN、PN,利用三角形中位线定理求出PM∥AD,PN∥AB,然后求出四边形AMPN是平行四边形,根据平行四边形的对边相等和直角三角形斜边上的中线等于斜边的一半求出CM=PN,PM=NE,再求出∠PMC=∠ENP,然后利用“边角边”证明△PMC和△ENP全等,根据全等三角形对应边相等可得PC=PE,全等三角形对应角相等可得∠PCM=∠EPN,然后求出∠CPE=∠CPM+∠PCM+∠PMB,再利用三角形内角和定理列式计算即可求出∠CPE=120°.
解答:解:(1)在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA),
∴BC=DE,
如图1,延长CP、ED,相交于点F,
∵P为线段BD的中点,
∴BP=DP,
∵∠ACB=∠AED=90°
∴BC∥DE,
∴∠F=∠BCP,
在△BCP和△DFP中,
,
∴△BCP≌△DFP(AAS),
∴CP=PF,BC=DF,
∴PC=PE=PF,
∴∠F=∠PEF,
又∵BC=DE=DF,AC=AE,
∴AD是△CEF的中位线,
∴AD∥CF,
∴∠F=∠ADE,
∵∠DAE=30°,∠AED=90°,
∴∠ADE=90°-30°=60°,
∴∠CPE=∠F+∠PEF=2∠F=2∠ADE=2×60°=120°;
(2)如图2,延长CP、ED,相交于点F,
∵P为线段BD的中点,
∴BP=DP,
∵∠ACB=∠AED=90°
∴BC∥DE,
∴∠F=∠BCP,
在△BCP和△DFP中,
,
∴△BCP≌△DFP(AAS),
∴CP=PF,BC=DF,
∴PC=PE=PF,
∴∠F=∠PEF,
∵∠ACB=∠AED=90°,∠BAC=∠DAE=30°,
∴AC=
BC,AE=
DE,
∴然后求出
=
=
,
∴AD∥CF,
∴∠F=∠ADE,
∴∠CPE=∠F+∠PEF=2∠F=2∠ADE=2×60°=120°;
(3)∠CPE=120°,PC=PE.
理由如下:如图3,取AB的中点M,AD的中点N,连接CM、PM、EN、PN,
∵P为线段BD的中点,
∴PM∥AD,PN∥AB,
∴四边形AMPN是平行四边形,
∴PM=AN,PN=AM,
∠AMA=∠PNA,
∴180°-∠AMA=180°-∠PNA,
即∠PMB=∠PND,
在Rt△ABC和Rt△ADE中,AM=CM,EN=AN,
∴CM=PN,PM=EN,
∠BMC=2∠BAC=2×30°=60°,
∠DNE=2∠DAE=2×30°=60°,
∴∠PMB+∠BMC=∠PND+∠DNE,
即∠PMC=∠ENP,
在△PMC和△ENP中,
,
∴△PMC≌△ENP(SAS),
∴PC=PE,∠PCM=∠EPN,
∵四边形AMPN的对边PN∥AM,
∴∠MPN=∠PMB,
∴∠CPE=∠CPM+∠MPN+∠EPN=∠CPM+∠PMB+∠PCM,
在△PMC中,∠CPM+∠PMB+∠PCM=180°-∠BMC=180°-60°=120°,
所以,∠CPE=120°.
|
∴△ABC≌△ADE(ASA),
∴BC=DE,
如图1,延长CP、ED,相交于点F,
∵P为线段BD的中点,
∴BP=DP,
∵∠ACB=∠AED=90°
∴BC∥DE,
∴∠F=∠BCP,
在△BCP和△DFP中,
|
∴△BCP≌△DFP(AAS),
∴CP=PF,BC=DF,
∴PC=PE=PF,
∴∠F=∠PEF,
又∵BC=DE=DF,AC=AE,
∴AD是△CEF的中位线,
∴AD∥CF,
∴∠F=∠ADE,
∵∠DAE=30°,∠AED=90°,
∴∠ADE=90°-30°=60°,
∴∠CPE=∠F+∠PEF=2∠F=2∠ADE=2×60°=120°;
(2)如图2,延长CP、ED,相交于点F,
∵P为线段BD的中点,
∴BP=DP,
∵∠ACB=∠AED=90°
∴BC∥DE,
∴∠F=∠BCP,
在△BCP和△DFP中,
|
∴△BCP≌△DFP(AAS),
∴CP=PF,BC=DF,
∴PC=PE=PF,
∴∠F=∠PEF,
∵∠ACB=∠AED=90°,∠BAC=∠DAE=30°,

∴AC=
| 3 |
| 3 |
∴然后求出
| AE |
| AC |
| DE |
| BC |
| DE |
| DF |
∴AD∥CF,
∴∠F=∠ADE,
∴∠CPE=∠F+∠PEF=2∠F=2∠ADE=2×60°=120°;
(3)∠CPE=120°,PC=PE.
理由如下:如图3,取AB的中点M,AD的中点N,连接CM、PM、EN、PN,
∵P为线段BD的中点,
∴PM∥AD,PN∥AB,
∴四边形AMPN是平行四边形,
∴PM=AN,PN=AM,
∠AMA=∠PNA,
∴180°-∠AMA=180°-∠PNA,
即∠PMB=∠PND,
在Rt△ABC和Rt△ADE中,AM=CM,EN=AN,
∴CM=PN,PM=EN,
∠BMC=2∠BAC=2×30°=60°,
∠DNE=2∠DAE=2×30°=60°,
∴∠PMB+∠BMC=∠PND+∠DNE,
即∠PMC=∠ENP,
在△PMC和△ENP中,
|
∴△PMC≌△ENP(SAS),
∴PC=PE,∠PCM=∠EPN,
∵四边形AMPN的对边PN∥AM,
∴∠MPN=∠PMB,
∴∠CPE=∠CPM+∠MPN+∠EPN=∠CPM+∠PMB+∠PCM,
在△PMC中,∠CPM+∠PMB+∠PCM=180°-∠BMC=180°-60°=120°,
所以,∠CPE=120°.
点评:本题是四边形综合题型,主要利用了全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,平行四边形的判定与性质,以及三角形的内角和定理,作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
二次函数y=x2的图象向上平移2个单位得到的图象的解析式为( )
| A、y=(x+2)2 |
| B、y=x2+2 |
| C、y=(x-2)2 |
| D、y=x2-2 |
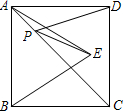 如图.正方形ABCD的面积为9,△ABE是等边三角形,点E在正方形ABCD内,P为对角线AC上一动点,使PD+PE最小,则这个最小值为
如图.正方形ABCD的面积为9,△ABE是等边三角形,点E在正方形ABCD内,P为对角线AC上一动点,使PD+PE最小,则这个最小值为 如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线
如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线
 如图,点P在∠AOB的内部.
如图,点P在∠AOB的内部.