题目内容
【题目】如图，抛物线y= 
x2+bx+c经过A（﹣1，0），C（2，﹣3）两点，与y轴交于点D，与x轴交于另一点B．
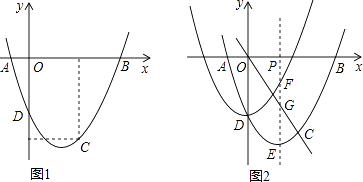
（1）求此抛物线的解析式及顶点坐标；
（2）若将此抛物线平移，使其顶点为点D，需如何平移？写出平移后抛物线的解析式；
（3）过点P（m，0）作x轴的垂线（1≤m≤2），分别交平移前后的抛物线于点E，F，交直线OC于点G，求证：PF=EG．
【答案】
（1）解：把A（﹣1，0），C（2，﹣3）代入y= 
x2+bx+c，
得： 
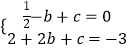，解得： 
，
∴抛物线的解析式为：y= x2﹣ 
x﹣2，
∵y= x2﹣ x﹣2= （x﹣ ）2﹣ 
，
∴其顶点坐标为：（ ， 
）
（2）解：∵y= x2﹣ x﹣2，
∴当x=0时，y=﹣2，
∴D点坐标为（0，﹣2）．
∵将点（ ， ）向左平移 个单位长度，再向上平移 
个单位长度，可得到点D，
∴将y= x2﹣ x﹣2向左平移 个单位长度，再向上平移 个单位长度，顶点为点D，
此时平移后的抛物线解析式为：y= x2﹣2
（3）证明：设直线OC的解析式为y=kx，
∵C（2，﹣3），
∴2k=﹣3，解得k=﹣ ，
∴直线OC的解析式为y=﹣ x．
当x=m时，yF= m2﹣2，则PF=﹣（ m2﹣2）=2﹣ m2，
当x=m时，yE= m2﹣ m﹣2，yG= 
，
则EG=yG﹣yE=2﹣ 
，
∴PF=EG．
【解析】（1）将A、C坐标分别代入函数解析式，建立二元一次方程组，求出b、c的值，就可以求出此函数的顶点坐标；
（2）此题考查了二次函数的平移，平移后的图像的顶点坐标D点坐标为（0，﹣2）．看得到平移后的函数解析式。图像平移前顶点坐标为（ ，- ），将图像平移就是将图像上的对应点移，将点（ ，- ）向左平移个单位长度，再向上平移 个单位长度，可得到点D（0，﹣2），可得出结论；（3）根据题意可知PE垂直于x轴，可知P、F、G三点的纵坐标相等，设P（m,0），点F在抛物线∵y= x2﹣2上，所以点F（m, m2﹣2），就可以用含m的代数式表示出PF=0-（m2﹣2）=2-m2，点G在直线OC上，求出直线OC的函数解析式为y=﹣ x，所以就点G（m,-m）点E在抛物线y= x2﹣ x﹣2上，E（m, m2﹣ m﹣2）,可以用含m的代数式表示出FG=﹣ m-（m2﹣ m﹣2）=2-m2，可得PF=EG．
【考点精析】掌握确定一次函数的表达式和二次函数图象的平移是解答本题的根本，需要知道确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减．
