题目内容
如图,∠A的顶点为A(0,3),两边分别经过点B(4,0)、C(0,-2).AD平分∠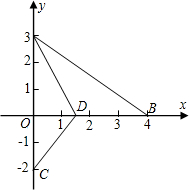 A并与x轴相交于点D,连接CD.
A并与x轴相交于点D,连接CD.(1)求证:BD=CD;
(2)求tan∠ACD的值.
分析:(1)由A(0,3),B(4,0),C(0,-2),即可求得AB的值,即可求得AB=AC,又由∠BAD=∠BAC,AD=AD,易证:△ABD≌△ACD,则根据全等三角形的性质即可证得BD=CD;
(2)由△ABD≌△ACD,可证得∠ACD=∠ABD,由三角函数的性质,即可求得tan∠ACD的值.
(2)由△ABD≌△ACD,可证得∠ACD=∠ABD,由三角函数的性质,即可求得tan∠ACD的值.
解答: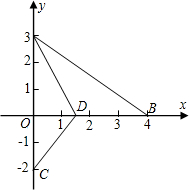 (1)证法一:∵A(0,3),B(4,0),C(0,-2),
(1)证法一:∵A(0,3),B(4,0),C(0,-2),
∴AB=
=5,AC=5,
∴AB=AC.
又∵∠BAD=∠BAC,AD=AD,
∴△ABD≌△ACD,
∴BD=CD.
证法二:过点D作DE⊥AB于E.
∵AD平分∠BAC,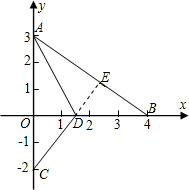
∴DO=DE,
设DO=DE=x,
∵∠ABO=∠ABO,
∴Rt△BED∽Rt△BOA.
∴
=
.
∵A(0,3),B(4,0),
∴AB=
=5,
∴
=
,
解得:x=
,即DO=
,
从而BD=4-
=
.
在Rt△BOD中,CD=
=
,
∴BD=CD.
证法三:∵A(0,3),B(4,0),C(0,-2),
∴AB=
=5,AC=5,
过点D作DE⊥AB于E.
∵AD平分∠BAC,
∴DO=DE,
∴EB=AB-AE=5-3=2=OC,
∴Rt△BED≌Rt△COD,
∴BD=CD.
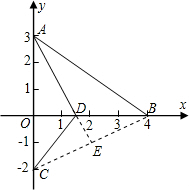
证法四:连接CB,延长AD交CB于E.
∵A(0,3),B(4,0),C(0,-2),
∴AB=
=5,AC=5,
∴AB=AC.
又∵AE平分∠BAC,
∴AE垂直平分CB,
∴BD=CD.
(2)解法一:∵△ABD≌△ACD,
∴∠ACD=∠ABD,
∴tan∠ACD=tan∠ABD=tan∠ABO=
=
.
解法二:设点D(x,0),则BD=CD=4-x,
在Rt△COD中,x2+22=(4-x)2,
解得:x=
.
∴D(
,0).
∴tan∠ACD=tan∠OCD=
=
=
.
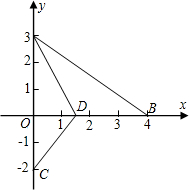 (1)证法一:∵A(0,3),B(4,0),C(0,-2),
(1)证法一:∵A(0,3),B(4,0),C(0,-2),∴AB=
| 32+42 |
∴AB=AC.
又∵∠BAD=∠BAC,AD=AD,
∴△ABD≌△ACD,
∴BD=CD.
证法二:过点D作DE⊥AB于E.
∵AD平分∠BAC,

∴DO=DE,
设DO=DE=x,
∵∠ABO=∠ABO,
∴Rt△BED∽Rt△BOA.
∴
| AB |
| DB |
| AD |
| DE |
∵A(0,3),B(4,0),
∴AB=
| 32+42 |
∴
| 5 |
| 4-x |
| 3 |
| x |
解得:x=
| 3 |
| 2 |
| 3 |
| 2 |
从而BD=4-
| 3 |
| 2 |
| 5 |
| 2 |
在Rt△BOD中,CD=
22+(
|
| 5 |
| 2 |
∴BD=CD.
证法三:∵A(0,3),B(4,0),C(0,-2),
∴AB=
| 32+42 |
过点D作DE⊥AB于E.
∵AD平分∠BAC,
∴DO=DE,
∴EB=AB-AE=5-3=2=OC,
∴Rt△BED≌Rt△COD,
∴BD=CD.

证法四:连接CB,延长AD交CB于E.
∵A(0,3),B(4,0),C(0,-2),
∴AB=
| 32+42 |
∴AB=AC.
又∵AE平分∠BAC,
∴AE垂直平分CB,
∴BD=CD.
(2)解法一:∵△ABD≌△ACD,
∴∠ACD=∠ABD,
∴tan∠ACD=tan∠ABD=tan∠ABO=
| OA |
| OB |
| 3 |
| 4 |
解法二:设点D(x,0),则BD=CD=4-x,
在Rt△COD中,x2+22=(4-x)2,
解得:x=
| 3 |
| 2 |
∴D(
| 3 |
| 2 |
∴tan∠ACD=tan∠OCD=
| OD |
| OC |
| ||
| 2 |
| 3 |
| 4 |
点评:此题考查了勾股定理,相似三角形的判定与性质,三角函数等知识.此题难度适中,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则sinα=
如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则sinα=
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).
21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).