Question

【题目】已知：抛物线y＝mx2+（m﹣2）x﹣2m+2（m≠0）．

（1）求证：抛物线与x轴有交点；

（2）若抛物线与x轴交于点A（x1，0），B（x2，0），点A在点B的右侧，且x1+2x2＝1．

①求m的值；

②点P在抛物线上，点G（n，﹣n﹣），求PG的最小值．

Answer 1

【答案】（1）见解析；（2）①m=1；②PG的最小值=

【解析】

（1）令y=0，再求出的方程的△是否大于等于0即可；

（2）①令y=0，解一元二次方程，再根据已知点A在点B的右侧，且，求解即可；②先假设与直线平行的直线l的关系式为,

若直线l与抛物线只有一个交点C,列方程，根据得b的值，则点C到直线的距离就是PG的最小值.

（1）当y=0时，

.

∴抛物线与x轴有交点;

（2）①当y=0时，,

解得或,

∵点A在点B的右侧,

∴,

∵，

∴ 当，时,1+2，解得m=1,

此时，，满足，故m=1符合题意,

当，时,，解得m=2.

此时，，与矛盾，故m=2不符合题意.

∴m=1;

②

当m=1时,抛物线解析式为 ,

∵点G,

∴点G在直线上.

假设与直线平行的直线l的关系式

为,

若直线l与抛物线只有一个交点C,

则此时方程 的,解得b=.

∴直线l的关系式 ,

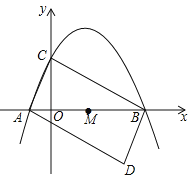
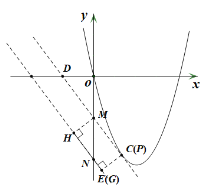
如图，直线l与x轴，y轴分别交于D，M两点，直线

与y轴交于N点，

∴D（，0），M（0，）.

∴OD=，OM=.

∴MN=，

DM== ，

过点M作MH⊥HN，CE⊥EN，当P点与C点重合，G点与E点重合时，PG长最小，

此时△MHN∽△DOM，

∴，即，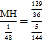

∴PG=MH=,

即PG的最小值是 .

故答案为：（1）见解析；（2）①m=1；②PG的最小值=.