Question

（本小题满分7分）
如图，矩形ABCD，AB＝4，AD＝3，动点M、N分别从D、B同时出发，以1个
单位/秒的速度运动，点M沿DA向终点A运动，点N沿BC向终点C运动。过点
N作NP⊥BC，交AC于点P，连结MP。已知动点M、N运动了秒．
⑴请直接写出PN的长；（用含的代数式表示）
⑵若0秒≤≤1秒，试求△MPA的面积S与时间秒的函数关系式，利用函数图
象，求S的最大值；
⑶若0秒≤≤3秒，△MPA能否为一个等腰三角形？若能，试求出所有的对应
值；若不能，试说明理由．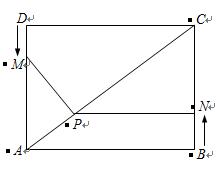

Answer 1

⑴；
⑵延长NP交AD于点Q，则PQ⊥AD，则，依题意，可得：

∵0≤≤1.5 即函数图象在对称轴的左侧，函数值S随着的增大而增大。∴当时，S有最大值 ，S_最大值＝。

⑶△MPA能成为等腰三角形，共有三种情况，以下分类说明：
①若PM＝PA，
∵PQ⊥MA   ∴MQ＝QA＝， 又DM＋MQ＋QA＝AD   ∴，即
②若MP＝MA，则MQ＝，PQ＝，MP＝MA＝
在Rt△PMQ中，由勾股定理得：
∴，解得：（不合题意，舍去）
③若AP＝AM，由题意可得：，AM＝，∴，解得：
综上所述，当，或，或时，△MPA是等腰三角形。

解析