题目内容
如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB边上,过点E作EF⊥BC,延长FE交⊙O的切线AG于点G.
(1)求证:GA=GE.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
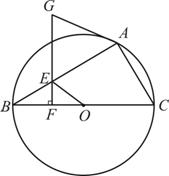
(1)证明:连接OA,
 ∵AG切⊙O点A,
∵AG切⊙O点A,
∴∠GAO=90°.
∴∠BAO+∠GAE=90°.………………………………………1
∵EF⊥BC,
∴∠ABO+∠BEF=90°.
∵OA=OB,
∴∠ABO=∠BAO.
∴∠GAE=∠BEF.
∵∠BEF=∠GEA,
∴∠GEA=∠GAE.
∴GA=GE.……………………………………………………2
(2)解:∵BC为直径,
∴∠BAC=90°,AC=6,AB=8,
∴BC=10,…………………………………………………………………………………………3
∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA,
∴
∴EF= ,BF=
,BF= ,
,
∴OF=OB﹣BF=5﹣ =
= ,……………………………………………………………………4
,……………………………………………………………………4
∴OE= .……………………………………………………………………5
.……………………………………………………………………5

练习册系列答案
相关题目
下表记录了一名球员在罚球线上投篮的结果.那么,这名球员下次投篮,投中的概率约是_________(精确到0.1).
| 投篮次数( | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
| 投中次数( | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
| 投中频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
 的图象,下列说法正确的是
的图象,下列说法正确的是
 )
) )
) )
) ,求
,求 的值.
的值. A. 4 B. 0 C. -2 D. -4
A. 4 B. 0 C. -2 D. -4 中,AB∥DC , AD∥BC,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是
中,AB∥DC , AD∥BC,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是 B.
B. C.
C. D.
D.
 的长.
的长. 
 ,则x-y= _.
,则x-y= _.