题目内容
某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q=W+100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.

(1)用含x和n的式子表示Q;
(2)当x=70,Q=450时,求n的值;
(3)若n=3,要使Q最大,确定x的值;
(4)设n=2,x=40,能否在n增加m%(m>0)
同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-![]() ,
,![]() )
)
答案:

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q=W+100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
| 次数n | 2 | 1 |
| 速度x | 40 | 60 |
| 指数Q | 420 | 100 |
(2)当x=70,Q=450时,求n的值;
(3)若n=3,要使Q最大,确定x的值;
(4)设n=2,x=40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420?若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-
 ,
, )
) 某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q =" W" + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
| 次数n | 2 | 1 |
| 速度x | 40 | 60 |
| 指数Q | 420 | 100 |
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是
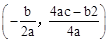
某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q=W+100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
(1)用含x和n的式子表示Q;
(2)当x=70,Q=450时,求n的值;
(3)若n=3,要使Q最大,确定x的值;
(4)设n=2,x=40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420?若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-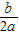 ,
,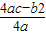 )
)
| 次数n | 2 | 1 |
| 速度x | 40 | 60 |
| 指数Q | 420 | 100 |
(2)当x=70,Q=450时,求n的值;
(3)若n=3,要使Q最大,确定x的值;
(4)设n=2,x=40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420?若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-
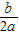 ,
,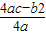 )
)某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q =" W" + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
|
次数n |
2 |
1 |
|
速度x |
40 |
60 |
|
指数Q |
420 |
100 |
(1)用含x和n的式子表示Q;
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是