题目内容
解方程：
（1）
；（2）
．
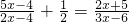解：（1）方程两边同乘x（x+1），
得：5x-4（x+1）=0，
整理得：5x-4x-4=0，
解得：x=4，
检验：将x=4代入x（x+1）=4×5=20≠0，
∴原方程的解为x=4；
（2）方程两边同乘6（x-2），
得3（5x-4）+3（x-2）=2（2x+5），
整理得：15x-12+3x-6=4x+10，
解得：x=2，
检验：将x=2代入6（x-2）=6（2-2）=0，
∴x=2是增根，
∴原方程无解．
分析：观察可得（1）中最简公分母为x（x+1）；
（2）中因为2x-4=2（x-2），3x-6=3（x-2），所以可确定最简公分母为6（x-2）．
点评：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．
（2）解分式方程一定注意要验根．
得：5x-4（x+1）=0，
整理得：5x-4x-4=0，
解得：x=4，
检验：将x=4代入x（x+1）=4×5=20≠0，
∴原方程的解为x=4；
（2）方程两边同乘6（x-2），
得3（5x-4）+3（x-2）=2（2x+5），
整理得：15x-12+3x-6=4x+10，
解得：x=2，
检验：将x=2代入6（x-2）=6（2-2）=0，
∴x=2是增根，
∴原方程无解．
分析：观察可得（1）中最简公分母为x（x+1）；
（2）中因为2x-4=2（x-2），3x-6=3（x-2），所以可确定最简公分母为6（x-2）．
点评：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．
（2）解分式方程一定注意要验根．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目