题目内容
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为

- A.1
- B.2
- C.3
- D.4
C
由抛物线的开口方向判断a与0的关系,由x=1时的函数值判断a+b+c>0,然后根据对称轴推出2a+b与0的关系,根据图象判断﹣1<x<3时,y的符号:
①∵图象开口向下,∴a<0。说法错误。
②∵对称轴为x= ,∴
,∴ ,即2a+b=0。说法正确。
,即2a+b=0。说法正确。
③当x=1时,y>0,则a+b+c>0。说法正确。
④由图可知,当﹣1<x<3时,y>0。说法正确。
∴说法正确的有3个。故选C。
由抛物线的开口方向判断a与0的关系,由x=1时的函数值判断a+b+c>0,然后根据对称轴推出2a+b与0的关系,根据图象判断﹣1<x<3时,y的符号:
①∵图象开口向下,∴a<0。说法错误。
②∵对称轴为x=
 ,∴
,∴ ,即2a+b=0。说法正确。
,即2a+b=0。说法正确。③当x=1时,y>0,则a+b+c>0。说法正确。
④由图可知,当﹣1<x<3时,y>0。说法正确。
∴说法正确的有3个。故选C。

练习册系列答案
相关题目
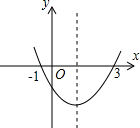 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<-1或x>3.其中,正确的说法有( )
如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<-1或x>3.其中,正确的说法有( )| A、①②④ | B、①②⑤ | C、①③⑤ | D、②④⑤ |
 8、已知:如图为二次函数y=ax2+bx+c的图象,则一次函数y=ax+b的图象不经过( )
8、已知:如图为二次函数y=ax2+bx+c的图象,则一次函数y=ax+b的图象不经过( )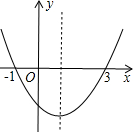 如图为二次函数y=ax2+bx+c(a≠0)的图象,下列说法中(1)ab<0;(2)a+b+c>0;(3)方程ax2+bx+c=0的根为x1=-1,x2=3;(4)当x>1时,y随x的增大而增大,正确的说法有
如图为二次函数y=ax2+bx+c(a≠0)的图象,下列说法中(1)ab<0;(2)a+b+c>0;(3)方程ax2+bx+c=0的根为x1=-1,x2=3;(4)当x>1时,y随x的增大而增大,正确的说法有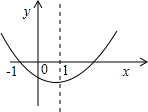 如图为二次函数y=ax2+bx+c的图象,则下列说法中正确的个数是( )
如图为二次函数y=ax2+bx+c的图象,则下列说法中正确的个数是( ) 如图为二次函数y=ax2+bx+c的图象,此图象与x轴的交点坐标分别为(-1,0)、(3,0).下列说法正确的个数是( )
如图为二次函数y=ax2+bx+c的图象,此图象与x轴的交点坐标分别为(-1,0)、(3,0).下列说法正确的个数是( )