Question

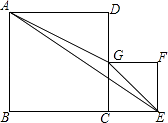
【题目】如图，四边形ABCD与四边形CEFG是两个正方形，边长分别为a、b．其中B、C、E在一条直线上，G在线段CD上．三角形AGE的面积为S．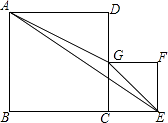

（1）①当a=5，b=3时，求S的值；
②当a=7，b=3时，求S的值；
（2）从以上结果中，请你猜想S与a、b中的哪个量有关？用字母a，b表示S，并对你的猜想进行证明．

Answer 1

【答案】
（1）

解：①∵四边形ABCD与四边形CEFG是两个正方形，AB=5，EC=3，

∴DG=CD﹣CG=5﹣3=2，

∴S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG

=25+9﹣ ×8×5﹣ ×5×2﹣ ×3×3=4.5，

②）①∵四边形ABCD与四边形CEFG是两个正方形，AB=7，EC=3，

∴DG=CD﹣CG=7﹣3=4，

∴S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG

=49+9﹣ ×10×7﹣ ×7×4﹣ ×3×3=4.5

（2）

解：结论S= b2．

证明：∵S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG

=a2+b2﹣ （a+b）a﹣ a（a﹣b）﹣ b2

=a2+b2﹣ a2﹣ ab﹣ a2+ ab﹣ b2

= b2．

∴S= b2

【解析】（1）①根据S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG即可解决问题．
②方法同上．（2）结论S= b2 ． 根据S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG即可证明．
【考点精析】关于本题考查的平行四边形的性质，需要了解平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能得出正确答案．