题目内容
在△ABC中,∠C=90°,D是AC上的点,∠A=∠DBC,将线段BD绕点B旋转,使点D落在线段AC的延长线上,记作点E,已知BC=2,AD=3,则DE=________.
2
分析:首先根据题意画出图形,判断出△ACB∽△BCD,即可求出CD的长,再利用三角形全等判定,得出Rt△CBE≌Rt△CBD,即可求出.
解答: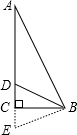 解:∵∠DCB=90°,∠A=∠DBC,
解:∵∠DCB=90°,∠A=∠DBC,
∴△ACB∽△BCD,
∴ ,
,
设DC=x,则AC=x+3,
∴ ,
,
解得:x=-4或x=1,
∵x表示线段DC长,
∴x=-4不合题意,舍去,
∴DC=1.
在Rt△CBE和Rt△CBD中,
BC=BC,BD=BE,
∴Rt△CBE≌Rt△CBD(HL),
∴DC=CE=1,
∴DE=2.
故答案为:2.
点评:此题主要考查了相似三角形的判定以及三角形全等的判定和旋转的性质,利用相似得出CD的长度是解决问题的关键.
分析:首先根据题意画出图形,判断出△ACB∽△BCD,即可求出CD的长,再利用三角形全等判定,得出Rt△CBE≌Rt△CBD,即可求出.
解答:
 解:∵∠DCB=90°,∠A=∠DBC,
解:∵∠DCB=90°,∠A=∠DBC,∴△ACB∽△BCD,
∴
 ,
,设DC=x,则AC=x+3,
∴
 ,
,解得:x=-4或x=1,
∵x表示线段DC长,
∴x=-4不合题意,舍去,
∴DC=1.
在Rt△CBE和Rt△CBD中,
BC=BC,BD=BE,
∴Rt△CBE≌Rt△CBD(HL),
∴DC=CE=1,
∴DE=2.
故答案为:2.
点评:此题主要考查了相似三角形的判定以及三角形全等的判定和旋转的性质,利用相似得出CD的长度是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于