题目内容
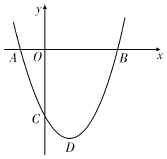
【题目】如图,已知拋物线![]() 经过A(-1,0),B(3,0)两点,与y轴相交于点C,该拋物线的顶点为点D.
经过A(-1,0),B(3,0)两点,与y轴相交于点C,该拋物线的顶点为点D.
(1)求该拋物线的解析式及点D的坐标;
(2)连接AC,CD,DB,BC,设△AOC,△BOC,△BCD的面积分别为 S1,S2,S3,求证:![]() .
.
(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN//BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时直线MN的解析式;若不存在,请说明理由.
【答案】(1)点D的坐标为(1,-4);(2)见解析(3)直线MN的解析式为![]() .
.
【解析】
试题
(1)由抛物线![]() 过点A(-1,0),B(3,0)可得其解析式为:
过点A(-1,0),B(3,0)可得其解析式为:![]() ,化简、再配方为顶点式,可得顶点D的坐标;
,化简、再配方为顶点式,可得顶点D的坐标;
(2)连接AC,CD,DB,BC,由(1)中所求解析式可得点C的坐标,这样就可由A、B、C、D、O五点的坐标分别求出三个三角形△AOC,△BOC,△BCD的面积,从而可证得:![]() .
.
(3)由题意可设点M的坐标为(m,0),其中-1<m<3,则AM=m+1;由已知和(2)可求得:AC=![]() ,AB=4;由MN∥BC可得:AM:AB=AN:AC,从而可得解得:AN=
,AB=4;由MN∥BC可得:AM:AB=AN:AC,从而可得解得:AN=![]() ;由∠AMN=∠ACM,∠MAN=∠CAM,可得△AMN∽△ACM,因此:AM:AC=AN:AM,由此可列出关于m的方程,解方程求得m的值即可得到点M的坐标,然后利用已知可求得直线BC的解析式,再由MN∥BC,即可求得直线MN的解析式.
;由∠AMN=∠ACM,∠MAN=∠CAM,可得△AMN∽△ACM,因此:AM:AC=AN:AM,由此可列出关于m的方程,解方程求得m的值即可得到点M的坐标,然后利用已知可求得直线BC的解析式,再由MN∥BC,即可求得直线MN的解析式.
试题解析:
(1)∵抛物线![]() 过点A(-1,0),B(3,0)
过点A(-1,0),B(3,0)
∴抛物线的解析式为y=(x+1)(x-3),即y=x2-2x-3.
∵y=x2-2x-3=(x-1)2-4,
∴点D的坐标为(1,-4)
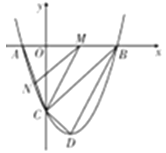
(2)如下图,
∵当x=0时,y=x2-2x-3=-3,
∴C(0,-3),
又∵A(-1,0),B(3,0),
∴![]() ,
,
![]() ,
,
![]() .
.
∴![]() .
.
∴△BCD为直角三角形,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
(3)存在点M使∠AMN=∠ACM.
设点M的坐标为(m,0)(-1<m<3),则MA=m+1,
![]() ,AB=1+3=4,
,AB=1+3=4,
∵MN//BC,
∴AM:AB=AN:AC,即(m+1):AN=4:![]() .
.
解得AN=![]() .
.
∵∠AMN=∠ACM,∠MAN=∠CAM,
∴△AMN∽△ACM.
∴AM:AC=AN:AM.即(m+1)2=![]() .
.
解得m1=-1(不合题意,舍去),![]() .
.
∴点M的坐标为![]() .
.
设直线BC的解析式为y=kx+b.
把B(3,0),C(0,-3)代入,得![]() 解得
解得![]()
∴直线BC的解析式为y=x-3.
又∵MN//BC,
∴设直线MN的解析式为y=x+n.
把点M的坐标![]() 代入,得
代入,得![]() .
.
∴直线MN的解析式为![]() .
.

 高中必刷题系列答案
高中必刷题系列答案