题目内容
如果一元二次方程x2-2 -3=0的两根为x1、x2,则x12x2+x1x22的值等于( )
-3=0的两根为x1、x2,则x12x2+x1x22的值等于( )
A、-6 B、6 C、-5 D、5
A
【解析】
试题分析:先根据根与系数的关系求出x1+x2和x1x2的值,再把它们的数值都代入所求代数式计算即可.
∵一元二次方程x2-2x-3=0的两根为x1、x2,
∴x1+x2=- =-
=- =2,x1x2=
=2,x1x2= =
= =-3,
=-3,
∴x12x2+x1x22=x1x2(x1+x2)=-3×2=-6.
故选A.
考点:根与系数的关系.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 D.
D.
 的图象如图所示,则下列结论:
的图象如图所示,则下列结论: ;
; 方程
方程 的两根之和大于0;
的两根之和大于0; ;④
;④ ,其中正确的个数( )
,其中正确的个数( )
 ,宽为3
,宽为3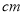 的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为
的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为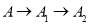 ,由
,由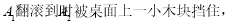 此时长方形木板的边
此时长方形木板的边 与桌面成30°角,则点A翻滚到A2位置时所经过的路径总长度为 cm.
与桌面成30°角,则点A翻滚到A2位置时所经过的路径总长度为 cm.
 的对称轴是( )
的对称轴是( ) B.
B. C.
C. D.
D.
 的根的情况是( )
的根的情况是( )