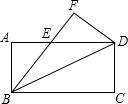
题目内容
阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为
+
.然后利用几何知识可知:当x=
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
+
的最小值为______.
| 16+(8-x)2 |
| 4+x2 |
| 8 |
| 3 |
| 25+(12-x)2 |
| 9+x2 |

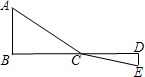
如图所示:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,
若AB=5,DE=3,BD=12,
当A,C,E,在一条直线上,AE最短,
∵AB⊥BD,ED⊥BD,
∴AB∥DE,
∴△ABC∽EDC,
∴
=
,
∴
=
,
解得:DC=
.
即当x=
时,代数式
+
的最小值,
此时为:
+
=
+
=4
.
故答案为:4
.

若AB=5,DE=3,BD=12,
当A,C,E,在一条直线上,AE最短,
∵AB⊥BD,ED⊥BD,
∴AB∥DE,
∴△ABC∽EDC,
∴
| AB |
| DE |
| BC |
| CD |
∴
| 5 |
| 3 |
| 12-CD |
| CD |
解得:DC=
| 9 |
| 2 |
即当x=
| 9 |
| 2 |
| 25+(12-x)2 |
| 9+x2 |
此时为:
25+(12-
|
9+(
|
5
| ||
| 2 |
3
| ||
| 2 |
| 13 |
故答案为:4
| 13 |


练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目