Question

【题目】已知二次函数的图象与轴分别交于点A、B（A左B右），与轴交于点C，顶点是P．

（1）则A点坐标是：________；B点坐标是：________；

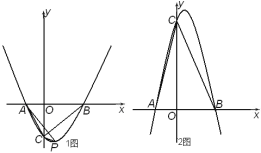
（2）当时，如1图所示：设△ACP的面积为，△ABC的面积为，求的值；

（3）当且∠ACB＝45°时，如2图所示：求此二次函数的解析式．

Answer 1

【答案】 （1）（-2，0），（3，0）；（2）；（3）．

【解析】（1）令y=0，解方程可得结论 ；

（2）连接OP，先求出C点坐标，P点坐标；然后分别求出的面积，即可得到结论；

（3）作AD⊥BC于D，交OC于E，设．通过证明△DCE≌△DAB，得到CE＝AB＝5，再由△OAE∽△OCB， 根据相似三角形对应边成比例，可求出OE、OC的长，从而得到点C的坐标，代入抛物线的解析式即可求出a的值，进而得出结论．

（1）令y=0，得：ax2-ax-6a=0，解得：x1=-2，x2=3，∴A（-2， 0）、B（3，0） ；

（2）如1图，连接OP，

先出C点坐标是，P点坐标是；

∴，

，

∴ ，

（3）如2图，作AD⊥BC于D，交OC于E，

设．

∵∠ACB＝45°，∴等腰直角△ADC，∴DC＝DA，

∴△DCE≌△DAB，∴CE＝AB＝5，

又∵△OAE∽△OCB，

∴，∴，∴舍）∴，

∴，∴点坐标是．

把代入，得，

∴此二次函数的解析式是．