题目内容
【题目】已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP. 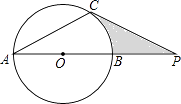
(1)求证:CP是⊙O的切线;
(2)若AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】
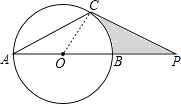
(1)解:如图,连接OC;
∵OA=OC,AC=CP,
∴∠A=∠OCA=30°,∠P=∠A=30°,
∴∠POC=∠A+∠OCA=60°,
∴∠OCP=180°﹣60°﹣30°=90°,
∴CP是⊙O的切线
(2)解:∵AB=4 ![]() ,
,
∴OC=OB=2 ![]() ,
,
∴PC= ![]() =6
=6
∴S△OCP= ![]() OCPC
OCPC
= ![]() ×2
×2 ![]() 6=6
6=6 ![]() ,
,
S扇形OBC= ![]() =2π,
=2π,
∴图中阴影部分的面积=6 ![]() ﹣2π
﹣2π
【解析】(1)如图,连接OC;运用已知条件证明∠OCP=90°,即可解决问题.(2)分别求出△OCP、扇形OCB的面积,即可解决问题.
【考点精析】本题主要考查了切线的判定定理和扇形面积计算公式的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

练习册系列答案
相关题目