题目内容
已知 ,求
,求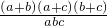 的值.
的值.
解:解法1:(1)若a+b+c≠0,由等比定理有
若
=
=1,
所以a+b-c=c,a-b+c=b,-a+b+c=a,
于是有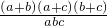 =
=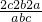 =8.
=8.
(2)若a+b+c=0,则a+b=-c,b+c=-a,c+a=-b,
于是有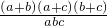 =
=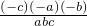 =-1.
=-1.
解法2:若 =k,
=k,
则a+b=(k+1)c,①
a+c=(k+1)b,②
b+c=(k+1)a.③
①+②+③有2(a+b+c)=(k+1)(a+b+c),
所以(a+b+c)(k-1)=0,
故有k=1或a+b+c=0.
当k=1时,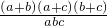 =
=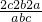 =8.
=8.
当a+b+c=0时,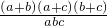 =
=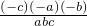 =-1.
=-1.
分析:根据比例的等比性质解决分式问题.注意分两种情况:a+b+c≠0;a+b+c=0进行讨论.本题还可以设参数法解答.
点评:本题考查了等比性质:若 ,则
,则 =k,(b+d+…+n≠0).特别注意条件的限制(分母是否为0).比例有一系列重要的性质,在解决分式问题时,灵活巧妙地使用,便于问题的求解.引进一个参数k表示以连比形式出现的已知条件,可使已知条件便于使用.
=k,(b+d+…+n≠0).特别注意条件的限制(分母是否为0).比例有一系列重要的性质,在解决分式问题时,灵活巧妙地使用,便于问题的求解.引进一个参数k表示以连比形式出现的已知条件,可使已知条件便于使用.
若

=

=1,
所以a+b-c=c,a-b+c=b,-a+b+c=a,
于是有
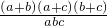 =
=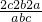 =8.
=8.(2)若a+b+c=0,则a+b=-c,b+c=-a,c+a=-b,
于是有
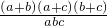 =
=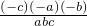 =-1.
=-1.解法2:若
 =k,
=k,则a+b=(k+1)c,①
a+c=(k+1)b,②
b+c=(k+1)a.③
①+②+③有2(a+b+c)=(k+1)(a+b+c),
所以(a+b+c)(k-1)=0,
故有k=1或a+b+c=0.
当k=1时,
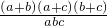 =
=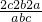 =8.
=8.当a+b+c=0时,
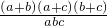 =
=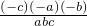 =-1.
=-1.分析:根据比例的等比性质解决分式问题.注意分两种情况:a+b+c≠0;a+b+c=0进行讨论.本题还可以设参数法解答.
点评:本题考查了等比性质:若
 ,则
,则 =k,(b+d+…+n≠0).特别注意条件的限制(分母是否为0).比例有一系列重要的性质,在解决分式问题时,灵活巧妙地使用,便于问题的求解.引进一个参数k表示以连比形式出现的已知条件,可使已知条件便于使用.
=k,(b+d+…+n≠0).特别注意条件的限制(分母是否为0).比例有一系列重要的性质,在解决分式问题时,灵活巧妙地使用,便于问题的求解.引进一个参数k表示以连比形式出现的已知条件,可使已知条件便于使用. 
练习册系列答案
相关题目
 ,求
,求 的值.
的值. ,求
,求 的值.
的值. ,求
,求 的值.
的值. ,求
,求 的值
的值 的值
的值
 ,求
,求 的值
的值