题目内容
已知：A=ax2+x-1，B=3x2-2x+1（a为常数）
（1）若A与B的和中不含x2项，求a的值．
（2）在（1）的基础上化简：B-2A，并求出当x=-1时，B-2A的值．
（1）若A与B的和中不含x2项，求a的值．
（2）在（1）的基础上化简：B-2A，并求出当x=-1时，B-2A的值．
分析：（1）A与B的和中不含x2项，即x2项的系数为0，依此求得a的值；
（2）先将表示A与B的式子代入B-2A，再去括号合并同类项．
（2）先将表示A与B的式子代入B-2A，再去括号合并同类项．
解答：解：（1）A+B=ax2+x-1+3x2-2x+1=（a+3）x2-x，
∵A与B的和中不含x2项，
∴a+3=0，
则a=-3；
（2）B-2A=3x2-2x+1-2×（-3x2+x-1）
=3x2-2x+1+6x2-2x+2
=9x2-4x+3，
当x=-1时，
原式=9-4×（-1）+3=10．
∵A与B的和中不含x2项，
∴a+3=0，
则a=-3；
（2）B-2A=3x2-2x+1-2×（-3x2+x-1）
=3x2-2x+1+6x2-2x+2
=9x2-4x+3，
当x=-1时，
原式=9-4×（-1）+3=10．
点评：本题考查了整式的加减，解答本题的关键是掌握多项式加减的运算法则，合并同类项的法则．
练习册系列答案
相关题目
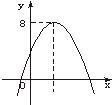9、已知抛物线y=ax2+bx+c如图所示，则关于x的方程ax2+bx+c-8=0的根的情况是（ ）
已知抛物线y=ax2+bx+c（a＞0）的图象经过点B（12，0）和C（0，-6），对称轴为x=2．
已知抛物线y=ax2+bx+c经过A（-1，0），B（3，0），C（0，3）三点．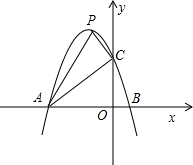
已知抛物线y=ax2+bx+c（a≠0）过点A（-3，0），B（1，0），C（0，3）三点
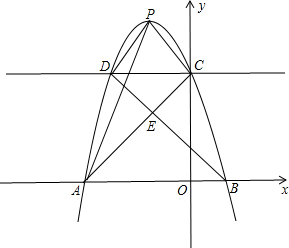（2012•瑶海区三模）已知抛物线y=ax2+bx+c（a≠0）过点A（-3，0），B（1，0），C（0，3）三点．