Question

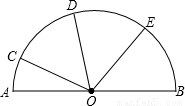
已知：如图，⊙O的半径为

2

，弦AB=2，点D是劣弧AB上任一点（与端点A、B不重合），DE⊥AB于点E，以点D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，切点为F、G，两条切线相交于点C．
（1）求∠AOB的度数；
（2）判断∠ACB是否为定值，若是，求出∠ACB的大小；否则，请说明理由；
（3）记△ABC的面积为y，DE的长为x，试求y与x的函数关系式，并确定自变量的取值范围．

Answer 1

分析：（1）由勾股定理的逆定理，易证∠AOB的度数为90°；
（2）连接AD、BD，由（1）和圆内接四边形的性质得，∠ADB=135°，根据点O是△ABC的内心，则∠ADB=90°+

1

2

∠C，从而得出∠ACB为定值；
（3）在直角三角形ABC中，∠C=90度，内切圆半径DE=x，斜边长AB=2．这样容易求出面积y与x关系．

解答：解：（1）∵OA=

2

，AB=2，
∴OA²+OB²=AB²，
∴△ABC为直角三角形，
∴∠AOB=90°；

（2）连接AD、BD，
∵∠AOB=90°，
∴∠ADB=135°，
∵⊙D是△ABC的内切圆，
∴∠ADB=90°+

1

2

∠C，
∴∠C=90°；

（3）设AC=b，BC=a，则有a+b=2+2x（切线长定理），
∵a²+b²=（a+b）²-2ab，
∴（2+2x）²-4y=4（勾股定理），
∴y=（x+1）²-1，
当DEO三点共线时，x最大，即x=

2

-1，
∴自变量x的取值范围是0＜x≤

2

-1．

点评：本题考查了三角形的内切圆和内心，勾股定理的逆定理，圆内接四边形的性质，是中考压轴题，难度较大．