题目内容
在钝角三角形ABC中，若AB=AC，D是BC上一点，AD把△ABC分成两个等腰三角形，则∠BAC的度数为
- A.150°
- B.124°
- C.120°
- D.108°
D
分析：从已知条件结合图形，利用等腰三角形的性质以及三角形内角和定理列出方程求解即可．
解答：
解：设∠ABC为x．
（180°-x）÷2+x+2x=180°
解得x=36°
∴180°-36°×2=108°．
故选D．
点评：本题考查等腰三角形的性质和三角形内角和定理，熟练掌握定理是解决本题的关键．题目比较简单，属于基础题．
分析：从已知条件结合图形，利用等腰三角形的性质以及三角形内角和定理列出方程求解即可．
解答：
解：设∠ABC为x．（180°-x）÷2+x+2x=180°
解得x=36°
∴180°-36°×2=108°．
故选D．
点评：本题考查等腰三角形的性质和三角形内角和定理，熟练掌握定理是解决本题的关键．题目比较简单，属于基础题．
练习册系列答案
相关题目
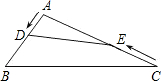如图，在钝角三角形ABC中，AB=6cm，AC=12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是（ ）
14、如图，在钝角三角形ABC中，AB=6cm，AC=12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是
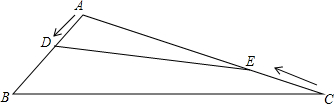
在钝角三角形△ABC中，已知点P在△ABC的边AB上，按下列给出的条件分别画出图形：