题目内容
如图,直角坐标系中,已知点A(2,4),B(5,0),动点P从B点出发沿BO向终点O运动,动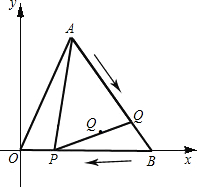 点Q从A点出发沿AB向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了xs.
点Q从A点出发沿AB向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了xs.(1)Q点的坐标为
(2)当x为何值时,△APQ是一个以AP为腰的等腰三角形?
(3)记PQ的中点为G.请你探求点G随点P,Q运动所形成的图形,并说明理由.
分析:(1)如果过点A作OB的垂线,不难求出cos∠ABO=
,sin∠ABO=
,因此,Q移动时,横向移动的速度是1•cos∠ABO=
单位/秒,纵向移动的速度是1•sin∠ABO=
单位/秒,因此Q得坐标就可表示为(2+
x,4-
x).
(2)有了A、Q的坐标,如果分别过A、Q做x轴的垂线,通过构成的直角三角形,不难用x表示出AQ、AP和PQ的值,然后分AP=AQ,PQ=AP两种情况进行讨论,得出x的值.
(3)通过观察G点似乎应该在三角形ABO的中位线上,因此它的轨迹应该是个线段.
可设AB、BO的中点分别为点M、N,设MN、PQ相交于点G′,只要证明G′与G重合,也就是G′是QP的中点即可.过点P作PK∥AO交AB于点K.只要证明KM=QM就行了,根据三角形AOB为等腰三角形,AQ、PK、MN都平行,不难得出AQ=BK,AM=BM,因此便可得出KM=QM了.由此便可得出G′是PQ中点,与G重合.
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
(2)有了A、Q的坐标,如果分别过A、Q做x轴的垂线,通过构成的直角三角形,不难用x表示出AQ、AP和PQ的值,然后分AP=AQ,PQ=AP两种情况进行讨论,得出x的值.
(3)通过观察G点似乎应该在三角形ABO的中位线上,因此它的轨迹应该是个线段.
可设AB、BO的中点分别为点M、N,设MN、PQ相交于点G′,只要证明G′与G重合,也就是G′是QP的中点即可.过点P作PK∥AO交AB于点K.只要证明KM=QM就行了,根据三角形AOB为等腰三角形,AQ、PK、MN都平行,不难得出AQ=BK,AM=BM,因此便可得出KM=QM了.由此便可得出G′是PQ中点,与G重合.
解答:解:(1)(2+
x,4-
x).
(2)由题意,得P(5-x,0),0<x≤5
由勾股定理
求得PQ2=(
x-3)2+(4-
x)2
AP2=(3-x)2+42
若AQ=AP,则x2=(3-x)2+42,解得x=
若PQ=AP
则(
x-3)2+(4-
x)2=(3-x)2+42
即
x2-10x=0,解得x1=0(舍去),x2=
经检验,当x=
或x=
时,△APQ是一个以AP为腰的等腰三角形.
(3)设AB、BO的中点分别为点M、N,则点G随点P、Q运动所形成的图形是线段MN
设MN,PQ相交于点G′,过点P作PK∥AO交AB于点K
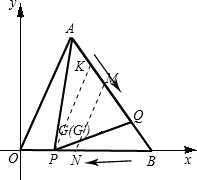
∴PK∥AO∥MN
∴△A0B∽△KPB∽△MNB.
∵AB=OB
∴BK=BP=AQ,BM=BN
∴BK-BM=AQ-BM,
BK-BM=AQ-AM
即KM=QM
∴PG′=QG′
∴G′是PQ的中点
即点G′与点G重合.
∴点G随点P、Q运动所形成的图形是△OBA的中位线MN.
| 3 |
| 5 |
| 4 |
| 5 |
(2)由题意,得P(5-x,0),0<x≤5
由勾股定理
求得PQ2=(
| 8 |
| 5 |
| 4 |
| 5 |
AP2=(3-x)2+42
若AQ=AP,则x2=(3-x)2+42,解得x=
| 25 |
| 6 |
若PQ=AP
则(
| 8 |
| 5 |
| 4 |
| 5 |
即
| 11 |
| 5 |
| 50 |
| 11 |
经检验,当x=
| 25 |
| 6 |
| 50 |
| 11 |
(3)设AB、BO的中点分别为点M、N,则点G随点P、Q运动所形成的图形是线段MN
设MN,PQ相交于点G′,过点P作PK∥AO交AB于点K

∴PK∥AO∥MN
∴△A0B∽△KPB∽△MNB.
∵AB=OB
∴BK=BP=AQ,BM=BN
∴BK-BM=AQ-BM,
BK-BM=AQ-AM
即KM=QM
∴PG′=QG′
∴G′是PQ的中点
即点G′与点G重合.
∴点G随点P、Q运动所形成的图形是△OBA的中位线MN.
点评:本题考查综合应用点的坐标,等腰三角形的判定等知识进行推理论证、运算及探究证明的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: