题目内容
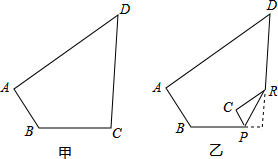 如图,(甲)是四边形纸片ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=
如图,(甲)是四边形纸片ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=90°
90°
.分析:根据两直线平行,同旁内角互补求出∠BPC和∠DRC,再根据翻折的性质求出∠CPR和∠CRP,然后利用三角形的内角和定理列式计算即可得解.
解答:解:∵CP∥AB,RC∥AD,
∴∠BPC=180°-∠B=180°-130°=50°,
∠DRC=180°-∠C=180°-50°=130°,
由翻折的性质,∠CPR=
(180°-∠BPC)=
(180°-50°)=65°,
∠CRP=
(180°-∠DRC)=
(180°-130°)=25°,
在△CPR中,∠C=180°-∠CPR-∠CRP=180°-65°-25°=90°.
故答案为:90°.
∴∠BPC=180°-∠B=180°-130°=50°,
∠DRC=180°-∠C=180°-50°=130°,
由翻折的性质,∠CPR=
| 1 |
| 2 |
| 1 |
| 2 |
∠CRP=
| 1 |
| 2 |
| 1 |
| 2 |
在△CPR中,∠C=180°-∠CPR-∠CRP=180°-65°-25°=90°.
故答案为:90°.
点评:本题考查了平行线的性质,翻折变换的性质,以及三角形的内角和定理,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
 下一个正确结论(或结果):
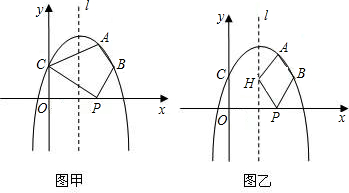
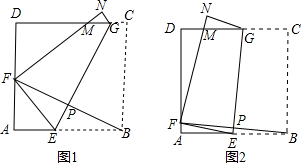
下一个正确结论(或结果): 如图,有甲乙两张纸条,甲纸条对折后与乙纸条宽度相等,将这两张纸条随意交叉重叠放在一起,重合的部分构成一个四边形ABCD,那么AB与BC的数量关系是
如图,有甲乙两张纸条,甲纸条对折后与乙纸条宽度相等,将这两张纸条随意交叉重叠放在一起,重合的部分构成一个四边形ABCD,那么AB与BC的数量关系是 如图,(甲)是四边形纸片ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=________.
如图,(甲)是四边形纸片ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=________.