题目内容
【题目】(本题满分![]() 分)
分)
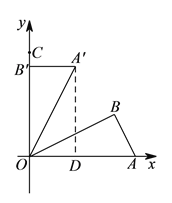
如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转至
按逆时针方向旋转至![]() ,
, ![]() 点的坐标为
点的坐标为![]() .
.

(![]() )求
)求![]() 点的坐标.
点的坐标.
(![]() )求过
)求过![]() ,
, ![]() ,
, ![]() 三点的抛物线
三点的抛物线![]() 的解析式.
的解析式.
(![]() )在(
)在(![]() )中的抛物线上是否存在点
)中的抛物线上是否存在点![]() ,使以
,使以![]() ,
, ![]() ,
, ![]() 为顶点的三角形是等腰直角三角形?若
为顶点的三角形是等腰直角三角形?若
存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】(![]() )过点
)过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,则四边形
,则四边形![]() 为矩形.
为矩形.
在![]() 中,
中, ![]() ,
,
![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(![]() )∵
)∵![]() 在抛物线上,
在抛物线上,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,在抛物线
,在抛物线![]() 上,
上,
∴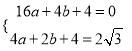 ,
,
解之得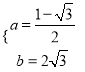 ,
,
∴所求解析式为![]() .
.
(![]() )①若以点
)①若以点![]() 为直角顶点,由于
为直角顶点,由于![]() ,
,
点![]() 在抛物线上,则点
在抛物线上,则点![]() 为满足条件的点.
为满足条件的点.
②若以点![]() 为直角顶点,则使
为直角顶点,则使![]() 为等腰直角三角形的点
为等腰直角三角形的点![]() 的坐标应为
的坐标应为![]() 或
或![]() ,代入抛物线解析式中知此两点不在抛物线上.
,代入抛物线解析式中知此两点不在抛物线上.
③若以点![]() 为直角顶点,则使
为直角顶点,则使![]() 为等腰直角三角形的点
为等腰直角三角形的点![]() 的坐标应为
的坐标应为![]() 或
或![]() ,代入抛物线解析式中知此两点不在抛物线上.
,代入抛物线解析式中知此两点不在抛物线上.
综上述在抛物线上只有一点![]() 使
使![]() 为等腰直角三角形.
为等腰直角三角形.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】一次期中考试中,甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)
甲 | 乙 | 丙 | 丁 | 戊 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:
标准分=(个人成绩一平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好,请问甲同学在本次考试中,数学与英语哪个学科考得更好?
