Question

班主任老师让同学们为班会活动设计一个抽奖方案，拟使中奖概率为60%．
（1）小明的设计方案：在一个不透明的盒子中，放入10个球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球则表示中奖，否则不中奖．如果小明的设计符合老师要求，则盒子中黄球应有______个，白球应有______个；
（2）小兵的设计方案：在一个不透明的盒子中，放入4个黄球和1个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球则表示中奖，否则不中奖．该设计方案是否符合老师的要求？试说明理由．

Answer 1

解：（1）∵班主任老师让同学们为班会活动设计一个抽奖方案，拟使中奖概率为60%，
∴在一个不透明的盒子中，放入10个球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球则表示中奖，即摸到黄球的概率为：60%，
设黄球为x个，则：
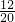=60%，
解得：x=6，故白球应有4个，
∴则盒子中黄球应有6个，白球应有4个；
故答案为：6，4；

（2）如下表所示：

	黄1	黄2	黄3	黄4	白
黄1		黄1黄2	黄1黄3	黄1黄4	黄1白
黄2	黄2黄1		黄2黄3	黄2黄4	黄2白
黄3	黄1黄3	黄2黄3		黄3黄4	黄3白
黄4	黄1黄4	黄2黄4	黄3黄4		黄4白
白	黄1白	黄2白	黄3白	黄4白

根据表格得到所有情况为20种，摸到的2个球都是黄球的情况一共有12种，
故摸到的2个球都是黄球的概率为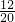：=60%，
故该设计方案符合老师的要求．
分析：（1）利用在一个不透明的盒子中，放入10个球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球则表示中奖，即摸到黄球的概率为：60%，
求出黄球个数即可得出答案．
（2）依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．
点评：本题考查了用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．