题目内容
如下图,已知C、D是锐角∠AOB的边OA上的两点,且OC=a,OD=b,在OB上求一点E,使∠CED取得最大值.

答案:
解析:
解析:
|
简解:作过C、D两点且与OB切于点E的圆.在OB上任取异于点E的一点 即点E离点O的距离为 分析:联想一条弧所对的圆周角和它所对的圆外角的关系,只要作出过C、D两点且与OB相切的圆,切点即为所求. 简评:由一条弧所对的圆周角与它所对的圆外角的关系,作出过点C、D两点且与OB相切的圆,确定了适合题意的点E的位置. |

练习册系列答案
相关题目
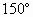 ,OB是∠AOC的平分线,OE,OF分别是∠AOB,∠BOC的平分线.
,OB是∠AOC的平分线,OE,OF分别是∠AOB,∠BOC的平分线.


