题目内容
 如图,CD是△ABC的角平分线,已知∠A=70°,∠B=40°,求∠ACD与∠BDC的度数.
如图,CD是△ABC的角平分线,已知∠A=70°,∠B=40°,求∠ACD与∠BDC的度数.
分析:根据三角形内角和定理求出∠ACB的度数,再根据CD是△ABC的角平分线,即可求出∠ACD的度数;再根据三角形内角和外角的关系即可求出∠BDC的度数.
解答:解:因为∠A=70°,∠B=40°,
所以∠ACB=180°-70°-40°=70°,
因为CD是△ABC的角平分线,
所以∠ACD=
∠ACB=
×70°=35°.
所以∠BDC=∠A+∠ACD=70°+35°=105°.
所以∠ACB=180°-70°-40°=70°,
因为CD是△ABC的角平分线,
所以∠ACD=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠BDC=∠A+∠ACD=70°+35°=105°.
点评:此题考查了三角形的内角和定义、角平分线的定义和三角形内角与外角的关系,是一道好题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.
26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.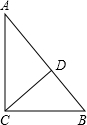 已知:如图,CD是△ABC的高,AC=4,BC=3,DB=
已知:如图,CD是△ABC的高,AC=4,BC=3,DB= 如图,CD是△ABC的中线,且CD=
如图,CD是△ABC的中线,且CD= 25、如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.
25、如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由. 如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.
如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.