题目内容
已知Rt△ABC，∠C=Rt∠，若以斜边AB为直径作⊙O，则点C在
- A.⊙O上
- B.⊙O内
- C.⊙O外
- D.不能确定
A
分析：要确定点与圆的位置关系，主要确定点与圆心的距离与半径的大小关系，若点到圆心的距离为d，圆的半径r，则d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．
解答：∵∠C=Rt∠，以斜边AB为直径作⊙O，
∴O为斜边AB的中点，
∴OC=
AB=r，
∴点C在圆上．
故选A．
点评：本题考查了对点与圆的位置关系的判断．解决此类题目的关键是首先确定点与圆心的距离，然后与圆的半径进行比较，进而得出结论．
分析：要确定点与圆的位置关系，主要确定点与圆心的距离与半径的大小关系，若点到圆心的距离为d，圆的半径r，则d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．
解答：∵∠C=Rt∠，以斜边AB为直径作⊙O，
∴O为斜边AB的中点，
∴OC=
AB=r，∴点C在圆上．
故选A．
点评：本题考查了对点与圆的位置关系的判断．解决此类题目的关键是首先确定点与圆心的距离，然后与圆的半径进行比较，进而得出结论．
练习册系列答案
全能测控期末小状元系列答案
相关题目
已知Rt△ABC中，∠C=90°，AC=8cm，BC=6cm．则其内心和外心之间的距离是（ ）
| A、10cm | ||
| B、5cm | ||
C、
| ||
| D、2cm |
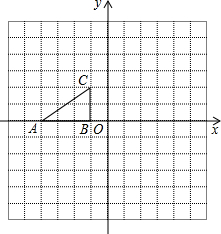如图，每个小方格都是边长为1个单位的正方形．Rt△ABC 的顶点在格 点上，建立平面直角坐标系后，点A的坐标为（-4，0），点B的坐标为（-1，0）．已知Rt△ABC和Rt△A1B1C1关于y轴对称，Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称．