题目内容
等腰梯形ABCD中,AD∥BC,BC=4| 2 |
| 2 |
 的顶点E在边BC上移动(不与点C重合),一直角边始终经过点A(如图),斜边与CD交于点F,设BE=x,CF=y
的顶点E在边BC上移动(不与点C重合),一直角边始终经过点A(如图),斜边与CD交于点F,设BE=x,CF=y(1)求证:△ABE∽△ECF;
(2)求y关于x的函数解析式,并求出当点E移动到什么位置时y的值最大,最大值是多少?
(3)连接AF,当△AEF为直角三角形时,求x的值;
(4)求点E移动过程中,△ADF外接圆半径的最小值.
分析:(1)由题意易证∠1=∠3,从而得出△ABE∽△ECF;
(2)由相似得出比例式,即可得出y是x的二次函数,求出y的最大值即可;
(3)分两种情况①∠EAF=90°时,②∠EFA=90°时,得出x的值;
(4)设△ADF外接圆半径为r,作FH⊥AD于H,由勾股定理可求出r的最小值.
(2)由相似得出比例式,即可得出y是x的二次函数,求出y的最大值即可;
(3)分两种情况①∠EAF=90°时,②∠EFA=90°时,得出x的值;
(4)设△ADF外接圆半径为r,作FH⊥AD于H,由勾股定理可求出r的最小值.
解答: 解:(1)∵∠AEF=∠B=∠C=45°,
解:(1)∵∠AEF=∠B=∠C=45°,
∴∠1+∠2=∠2+∠3=135°,
∴∠1=∠3,
∴△ABE∽△ECF;
(2)AB=(4
-
)÷2×
=3,
由(1)得,
=
,即
=
,
∴y=
x(4
-x)=-
x2+
x(0<x<4
),
当x=2
即E为BC的中点时,ymax=
;
(3)(i)如图i.当∠EAF=90°时,EF=
AE,
∴EC=
AB,即4
-x=
×3,
∴x=
;
(ii)如图ii:∠EFA=90°时,∴AE=
EF,
∴AB=
EC,即3=
(4
-x),
∴x=
(4)设△ADF外接圆的圆心为O,其半径为r.
∵∠ADF=135°,
∴劣弧AF所对圆周角为45°
∴劣弧AF所对圆心角∠AOF=90°,
∴AF=
r,
当AF最小时,r也最小;
又∵当CF最大时,AF最小,
此时DF=DC-CF=3-
=
,
作FH⊥AD于H,则FH=DH=
,
∴AFmin=
=
=
,
∴rmin=
.
 解:(1)∵∠AEF=∠B=∠C=45°,
解:(1)∵∠AEF=∠B=∠C=45°,∴∠1+∠2=∠2+∠3=135°,
∴∠1=∠3,
∴△ABE∽△ECF;
(2)AB=(4
| 2 |
| 2 |
| 2 |
由(1)得,
| BE |
| CF |
| AB |
| CE |
| x |
| y |
| 3 | ||
4
|
∴y=
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
4
| ||
| 3 |
| 2 |

当x=2
| 2 |
| 8 |
| 3 |
(3)(i)如图i.当∠EAF=90°时,EF=
| 2 |
∴EC=
| 2 |
| 2 |
| 2 |
∴x=
| 2 |
(ii)如图ii:∠EFA=90°时,∴AE=
| 2 |

∴AB=
| 2 |
| 2 |
| 2 |
∴x=
| 5 |
| 2 |
| 2 |
(4)设△ADF外接圆的圆心为O,其半径为r.
∵∠ADF=135°,
∴劣弧AF所对圆周角为45°
∴劣弧AF所对圆心角∠AOF=90°,
∴AF=
| 2 |
当AF最小时,r也最小;

又∵当CF最大时,AF最小,
此时DF=DC-CF=3-
| 8 |
| 3 |
| 1 |
| 3 |
作FH⊥AD于H,则FH=DH=
| ||
| 6 |
∴AFmin=
| AH2+FH2 |
| 10 |
| 6 |
| 5 |
| 3 |
∴rmin=
5
| ||
| 6 |
点评:本题考查了相似三角形的判定和性质、二次函数的最值问题以及等腰梯形的性质,是一道综合题,难度较大.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目

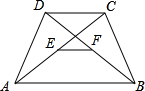 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积. (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°, 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是