题目内容

如图，一张长为10cm，宽为 $数学公式$ cm的矩形纸片ABCD如图，点P为AD的中点．沿PS将纸片折叠，使∠APQ=60°．若把折叠后的纸片平放在桌面上，则盖住桌面的面积为

A.
$数学公式$ cm²
B.
$数学公式$ cm²
C.
$数学公式$ cm²
D.
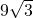$数学公式$ cm²

C
分析：由折叠可得重叠部分的面积为一个等边三角形，那么盖住桌面的面积为矩形的面积减去等边三角形的面积．
解答：

由折叠可得∠1=∠2，
∵∠APQ=60°．
∴∠EPC=∠2=60°，
∵AD∥BC，
∴∠PEC=∠APQ=60°，
∴△PES为等边三角形，
作PF⊥BC于点F，则PF= $\text{[math]}$ ，
∴ES=2FS=2，
∴盖住桌面的面积为：10× $\text{[math]}$ - $\text{[math]}$ × $\text{[math]}$ ×2=9 $\text{[math]}$ cm²．
故选C．
点评：考查折叠问题；得到住桌面的面积的关系式是解决本题的关键；判断出重叠部分的图形的形状是解决本题的突破点．