题目内容
如图所示,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.

(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?

(1) y=x2-3x+2;(2)存在,理由见解析;(3)当t=1时,S△BCN的最大值为1.
【解析】
试题分析:(1)已知了C点的坐标,即可得到OC的长,根据∠OAC的正切值即可求出OA的长,由此可得到A点的坐标,将A、C的坐标代入抛物线中,即可确定该二次函数的解析式;
(2)根据抛物线的解析式即可确定其对称轴方程,由此可得到点P的横坐标;若∠APC=90°,则∠PAE和∠CPD是同角的余角,因此两角相等,则它们的正切值也相等,由此可求出线段PE的长,即可得到点P点的坐标;(用相似三角形求解亦可)
(3)根据B、C的坐标易求得直线BC的解析式,已知了点M的横坐标为t,根据直线BC和抛物线的解析式,即可用t表示出M、N的纵坐标,由此可求得MN的长,以MN为底,B点横坐标的绝对值为高,即可求出△BNC的面积(或者理解为△BNC的面积是△CMN和△MNB的面积和),由此可得到关于S(△BNC的面积)、t的函数关系式,根据所得函数的性质即可求得S的最大值及对应的t的值.
试题解析::(1)∵抛物线y=x2+bx+c过点C(0,2),
∴x=2;
又∵tan∠OAC= =2,
=2,
∴OA=1,即A(1,0);
又∵点A在抛物线y=x2+bx+2上,
∴0=12+b×1+2,b=-3;
∴抛物线对应的二次函数的解析式为y=x2-3x+2;
(2)存在.
过点C作对称轴l的垂线,垂足为D,如图所示,

∴x=- ;
;
∴AE=OE-OA= ,
,
∵∠APC=90°,
∴tan∠PAE=tan∠CPD,
∴ ,
,
即  ,
,
解得PE= 或PE=
或PE= ,
,
∴点P的坐标为( ,
, )或(
)或( ,
, ).
).
(3)如图所示,易得直线BC的解析式为:y=-x+2,

∵点M是直线l′和线段BC的交点,
∴M点的坐标为(t,-t+2)(0<t<2),
∴MN=-t+2-(t2-3t+2)=-t2+2t,
∴S△BCN=S△MNC+S△MNB= MN▪t+
MN▪t+ MN▪(2-t)=
MN▪(2-t)= MN▪(t+2-t)=MN=-t2+2t(0<t<2),
MN▪(t+2-t)=MN=-t2+2t(0<t<2),
∴S△BCN=-t2+2t=-(t-1)2+1,
∴当t=1时,S△BCN的最大值为1.
考点: 二次函数综合题

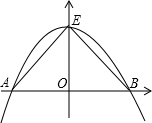 如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )
如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )| A、b=0 | B、S△ABE=c2 | C、ac=-1 | D、a+c=0 |
 (2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0). (2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).
(2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).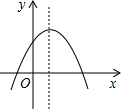 (1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( )
(1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( ) (1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;
(1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;