题目内容
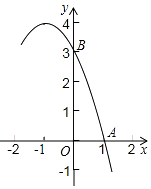
【题目】如图所示，平面直角坐标系中，△ABC的边AB在x轴上，∠C=60°，AC交y轴于点E，AC，BC的长是方程x2﹣16x+64=0的两个根且OA：OB=1：3，请解答下列问题：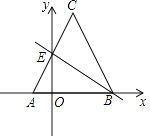
（1）求点C的坐标；
（2）求直线EB的解析式；
（3）在x轴上是否存在点P，使△BEP为等腰三角形？若存在，请直接写出点P的坐标，若不存在，请说明理由．
【答案】
（1）
解：解方程x2﹣16x+64=0得x1=8，x2=8，
∴AC=BC=8，
∵∠A=60°，
∴△ABC是等边三角形，
∴AB=8，
∵OA：OB=1：3，
∴AO=2，OB=6，
过点C作CH⊥x轴于点H，则AH= 
AB=4，CH= 
AB=4 
，
∴OH=AH﹣AO=4﹣2=2，
∴C（2，4 ）
（2）
解：设直线AE解析式为y=kx+b（k≠0），把A（﹣2，0）、C（2，4 ）代入可得 
，解得 
，
∴直线AC的解析式为y= x+2 ，
令x=0可得y=2 ，
∴E（0，2 ），
∵B（6，0），
设直线BE的解析式为y=rx+s，
∴ 
，解得 
，
∴直线BE的解析式为y=﹣ 
x+2
（3）
解：设P点坐标为（x，0），
∵B（6，0），E（0，2 ），
∴BE= 
=4 ，BP=|x﹣6|，PE= 
= 
，
若△BEP为等腰三角形，则有BP=EP、BP=BE和EP=BE三种情况，
② 当BP=EP时，则|x﹣6|= ，解得x=2，此时P点坐标为（2，0）；
②当BP=BE时，则4 =|x﹣6|，解得x=6+4 或x=6﹣4 ，此时P点坐标为（6+4 ，0）或（6﹣4 ，0）；
③当EP=BE时，则 =4 ，解得x=6或x=﹣6，当x=6时，点E和点B重合，不合题意，舍去，
∴x=﹣6，此时P点坐标为（6，0）；
综上可知存在满足条件的点P，其坐标为（2，0）或（6+4 ，0）或（6﹣4 ，0）或（6，0）．
【解析】（1）解方程x2﹣16x+64=0，可得到AC=BC=8，进而证得△ABC是等边三角形，得到AB=8，再由OA：OB=1：3，得到OA、OB的长，从而求得A、B的坐标即可求得C的坐标；（2）应用待定系数法即可求得直线AC的解析式，从而求得E的坐标，然后再根据待定系数法即可求得直线EB的解析式；（3）可设P点坐标为（x，0），则可表示出BP、EP，且可求得BE的长，当△BEP为等腰三角形时，则有BP=EP、BP=BE和EP=BE三种情况，可分别得到关于x的方程，可求得x的值，则可求得P点坐标．
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对等腰三角形的性质的理解，了解等腰三角形的两个底角相等（简称：等边对等角）．
