题目内容
在Rt△ABC中，已知AB=6，AC=8，∠A=90度．如果把Rt△ABC绕直线AC旋转一周得到一个圆锥，其表面积为S1；把Rt△ABC绕直线AB旋转一周得到另一个圆锥，其表面积为S2，那么S1：S2等于（ ）
| A、2：3 | B、3：4 | C、4：9 | D、5：12 |
分析：面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2，把相应数值代入后比较即可．
解答：解：∵AB=6，AC=8，∠A=90°，∴BC=10，斜边上的高=
，
∴绕直线AC旋转一周得到一个圆锥的底面周长=12π，侧面面积=60π，底面面积=36π，全面积S1=96π；
绕直线AB旋转一周得到一个圆锥的底面周长=16π，侧面面积=80π，底面面积=64π，全面积S2=144π；
∴S1：S2=2：3，故选A．
| 24 |
| 5 |
∴绕直线AC旋转一周得到一个圆锥的底面周长=12π，侧面面积=60π，底面面积=36π，全面积S1=96π；
绕直线AB旋转一周得到一个圆锥的底面周长=16π，侧面面积=80π，底面面积=64π，全面积S2=144π；
∴S1：S2=2：3，故选A．
点评：本题利用了勾股定理，圆的面积公式，圆的周长公式和扇形面积公式求解．
练习册系列答案
相关题目
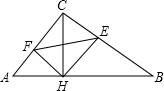如图，在Rt△ABC中，已知∠ACB=90°，且CH⊥AB，HE⊥BC，HF⊥AC．
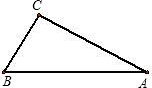如图，在Rt△ABC中，已知∠BCA=90°，∠BAC=30°，AB=6cm．把△ABC以点B为中心逆时针旋转，使点C旋转到AB边的延长线上得到Rt△A1BC1．在Rt△ABC中，已知∠C=90°，∠A=30°，BD是∠B的平分线，AC=18，则BD的值为（ ）
A、3
| ||
| B、9 | ||
| C、12 | ||
| D、6 |
如图，在Rt△ABC中，已知∠ABC=90°，BC=6，以AB为直径作⊙O，连接OC，过点C作⊙O的切线CD，D为切点，若sin∠OCD=
如图，在Rt△ABC中，已知tanB=2，则sinA的值是（ ）