جâؤ؟ؤعبف
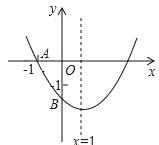
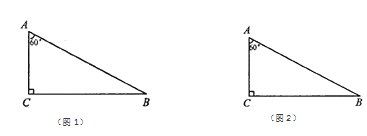
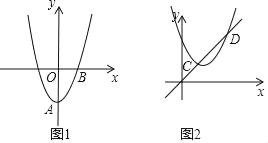
،¾جâؤ؟،؟بçح¼1£¬شعئ½أوض±½ا×ّ±êدµضذ£¬إ×خïدكC1£؛y=ax2+bx©پa2¹طسعyضل¶ش³ئازسذ×îذ،ضµ©پ1£®
£¨1£©اَإ×خïدكC1µؤ½âخِت½£»
£¨2£©شعح¼1ضذإ×خïدكC1¶¥µمخھA£¬½«إ×خïدكC1بئ µمBذ×ھ180،م؛َµأµ½إ×خïدكC2£¬ض±دكy=kx©پ2k+4×ـ¾¹ز»¶¨µمM£¬بô¹¶¨µمMµؤض±دكسëإ×خïدكC2ض»سذز»¸ِ¹«¹²µم£¬اَض±دكlµؤ½âخِت½£®
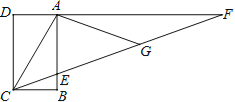
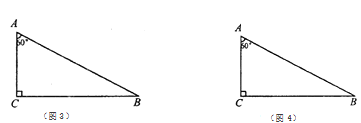
£¨3£©بçح¼2£¬دب½«إ×خïدك C1دٍةدئ½زئت¹ئن¶¥µمشعشµمO£¬شظ½«ئن¶¥µمرطض±دكy=xئ½زئµأµ½إ×خïدكC3£¬ةèإ×خïدكC3سëض±دكy=x½»سعC،¢Dء½µم£¬اَدك¶خCDµؤ³¤£®
،¾´ً°¸،؟£¨1£©y=x2©پ1£¨2£©¹¶¨µمM£¬¹²سذبجُض±دكl£؛x=2 »ٍy=2![]() x+4©پ4
x+4©پ4![]() »ٍy=©پ2
»ٍy=©پ2![]() x+4+4
x+4+4![]() £¬ثüأا·ض±ًسëإ×خïدكC3ض»سذز»¸ِ¹«¹²µم£¨3£©
£¬ثüأا·ض±ًسëإ×خïدكC3ض»سذز»¸ِ¹«¹²µم£¨3£©![]()
،¾½âخِ،؟تشجâ·ضخِ£؛ ![]() ¸ù¾فإ×خïدكµؤ¶ش³ئضلخھ
¸ù¾فإ×خïدكµؤ¶ش³ئضلخھ![]() ضل£¬اَµأ
ضل£¬اَµأ![]() إ×خïدكسذ×îذ،ضµ£¬؟ةاَµأ
إ×خïدكسذ×îذ،ضµ£¬؟ةاَµأ![]() £¬¼´؟ةاَ³ِإ×خïدك
£¬¼´؟ةاَ³ِإ×خïدك![]() µؤ½âخِت½.
µؤ½âخِت½.
![]() زہجâزâ؟ةاَ³ِإ×خïدك
زہجâزâ؟ةاَ³ِإ×خïدك![]() µؤ½âخِت½خھ£؛
µؤ½âخِت½خھ£؛ ![]() سةض±دك
سةض±دك![]() ×ـ¾¹ز»¶¨µمM£¬؟ةاَµأ¶¨µمMخھ
×ـ¾¹ز»¶¨µمM£¬؟ةاَµأ¶¨µمMخھ![]() £¬¢ظ¾¹¶¨µم
£¬¢ظ¾¹¶¨µم![]() سë
سë![]() ضلئ½ذذµؤض±دك
ضلئ½ذذµؤض±دك![]() £؛
£؛ ![]() سëإ×خïدك
سëإ×خïدك![]() ×ـسذز»¸ِ¹«¹²µم
×ـسذز»¸ِ¹«¹²µم![]() £®¢ع¾¹¶¨µم
£®¢ع¾¹¶¨µم![]() µؤض±دك
µؤض±دك![]() خھز»´خ؛¯ت
خھز»´خ؛¯ت![]() ت±£¬سë
ت±£¬سë![]() ءھء¢·½³ج×飬ہûسأ
ءھء¢·½³ج×飬ہûسأ![]() ؟ةµأµأ
؟ةµأµأ![]() µؤضµ£¬¼´؟ةµأ³ِ
µؤضµ£¬¼´؟ةµأ³ِ![]() »ٍ
»ٍ![]() £¬×غةدثùتِ£¬¹¶¨µمM£¬¹²سذبجُض±دكثüأا·ض±ًسëإ×خïدك
£¬×غةدثùتِ£¬¹¶¨µمM£¬¹²سذبجُض±دكثüأا·ض±ًسëإ×خïدك![]() ض»سذز»¸ِ¹«¹²µم£®
ض»سذز»¸ِ¹«¹²µم£®
![]() ةèإ×خïدك
ةèإ×خïدك![]() µؤ¶¥µمخھ
µؤ¶¥µمخھ![]() £¬زہجâزâ؟ةµأإ×خïدك
£¬زہجâزâ؟ةµأإ×خïدك![]() µؤ½âخِت½خھ£؛
µؤ½âخِت½خھ£؛ ![]() سëض±دك
سëض±دك![]() ءھء¢£¬؟ةµأ
ءھء¢£¬؟ةµأ![]() µؤ×ّ±ê£¬¹µمC×÷
µؤ×ّ±ê£¬¹µمC×÷![]() ،خ
،خ![]() ضل£¬¹µمD×÷DM،خyضل£¬؟ةاَ³ِ
ضل£¬¹µمD×÷DM،خyضل£¬؟ةاَ³ِ![]() ¼´؟ةµأ³ِ
¼´؟ةµأ³ِ![]() µؤضµ£®
µؤضµ£®
تشجâ½âخِ£؛£¨1£©![]() إ×خïدكµؤ¶ش³ئضلخھ
إ×خïدكµؤ¶ش³ئضلخھ![]() ضل£¬
ضل£¬
![]() ½âµأ
½âµأ![]()
![]() إ×خïدكµؤ½âخِت½خھ
إ×خïدكµؤ½âخِت½خھ![]()
![]() µ±
µ±![]() إ×خïدكسذ×îذ،ضµ£¬¼´
إ×خïدكسذ×îذ،ضµ£¬¼´![]() ½âµأ£؛
½âµأ£؛ ![]() »ٍ
»ٍ![]() £¨ةلب¥£©£®
£¨ةلب¥£©£®
إ×خïدك![]() µؤ½âخِت½
µؤ½âخِت½![]()
£¨2£©إ×خïدك![]() µؤ½âخِت½
µؤ½âخِت½![]()
![]()
ةèإ×خïدك![]() سëxضلµؤءîز»¸ِ½»µمخھ
سëxضلµؤءîز»¸ِ½»µمخھ![]() £®
£®
ءî![]() µأ£؛
µأ£؛ ![]() ½âµأ£؛
½âµأ£؛ ![]()
![]()
½«إ×خïدك![]() بئµم
بئµم![]() ذ×ھ
ذ×ھ![]() ؛َµأµ½إ×خïدك
؛َµأµ½إ×خïدك![]() £¬
£¬
،àµم![]() ¶شس¦µمµؤ×ّ±êخھ
¶شس¦µمµؤ×ّ±êخھ![]() £¬µم
£¬µم![]() ¶شس¦µمµؤ×ّ±êخھ
¶شس¦µمµؤ×ّ±êخھ![]() .
.
ةè![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ![]() ½«
½«![]() ´ْبëµأ£؛
´ْبëµأ£؛ ![]() ½âµأ
½âµأ![]()
![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ![]()
ض±دك![]() ×ـ¾¹ز»¶¨µمM£¬
×ـ¾¹ز»¶¨µمM£¬
،ඨµمMخھ![]() £¬
£¬
¢ظ¾¹¶¨µم![]() سë
سë![]() ضلئ½ذذµؤض±دك
ضلئ½ذذµؤض±دك![]() £؛
£؛ ![]() سëإ×خïدك
سëإ×خïدك![]() ×ـسذز»¸ِ¹«¹²µم
×ـسذز»¸ِ¹«¹²µم![]() £®
£®
¢ع½«![]() سë
سë![]() ءھء¢µأ£؛
ءھء¢µأ£؛ ![]() صûہيµأ£؛
صûہيµأ£؛ ![]()
،ك¹¶¨µمMµؤض±دكسëإ×خïدك![]() ض»سذز»¸ِ¹«¹²µم£¬
ض»سذز»¸ِ¹«¹²µم£¬
![]() ½âµأ
½âµأ![]()
،๶¨µمMµؤض±دكµؤ½âخِت½خھ![]() »ٍ
»ٍ![]() £¬
£¬
×غةدثùتِ£¬¹¶¨µمM£¬¹²سذبجُض±دكl£؛ ![]() »ٍ
»ٍ![]() »ٍ
»ٍ![]() £¬ثüأا·ض±ًسëإ×خïدك
£¬ثüأا·ض±ًسëإ×خïدك![]() ض»سذز»¸ِ¹«¹²µم£®
ض»سذز»¸ِ¹«¹²µم£®
£¨3£©زشئ½زئ؛َإ×خïدكµؤ¶¥µمخھ×ّ±êشµم½¨ء¢×ّ±êدµ£¬شٍض±دك؛حإ×خïدكشعذآ×ّ±êدµµؤ½âخِت½خھ![]() سë
سë![]()
½«![]() سë
سë![]() ءھء¢£¬½âµأ£؛
ءھء¢£¬½âµأ£؛ ![]() »ٍ
»ٍ![]()
،àµم![]() ؛حµم
؛حµم![]() شعذآ×ّ±êدµؤعµؤ×ّ±ê·ض±ًخھ
شعذآ×ّ±êدµؤعµؤ×ّ±ê·ض±ًخھ![]()
![]()