题目内容
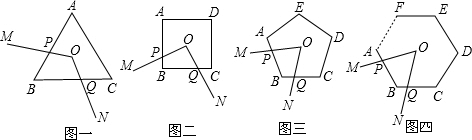
 如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角两边分别交AB,AC边于M,N两点,连接MN.
如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角两边分别交AB,AC边于M,N两点,连接MN.( I)探究:线段BM,MN,NC之间的关系,并加以证明.
(Ⅱ)若点M是AB的延长线上的一点,N是CA的延长线上的点,其它条件不变,请你再探线段BM,MN,NC之间的关系,在图②中画出图形,并说明理由.
分析:(1)延长AC至E,使得CE=BM并连接DE,构造全等三角形,找到相等的线段,MD=DE,再进一步证明△DMN≌△DEN,进而得到MN=BM+NC.
(2)按要求作出图形,先证△BMD≌△CED,再证△MDN≌△EDN(SAS),即可得出结论.
(2)按要求作出图形,先证△BMD≌△CED,再证△MDN≌△EDN(SAS),即可得出结论.
解答:解:(1)MN=BM+NC.理由如下:
延长AC至E,使得CE=BM(或延长AB至E,使得BE=CN),并连接DE.
∵△BDC为等腰三角形,△ABC为等边三角形,
∴BD=CD,∠DBC=∠DCB,∠MBC=∠ACB=60°,
又BD=DC,且∠BDC=120°,
∴∠DBC=∠DCB=30°
∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°,
∴∠MBD=∠ECD=90°,
在△MBD与△ECD中,
∵
,
∴△MBD≌△ECD(SAS),
∴MD=DE,
∴△DMN≌△DEN,
∴MN=BM+NC.
(2)按要求作出图形,(1)中结论不成立,应为MN=NC-BM.
在CA上截取CE=BM.
∵△ABC是正三角形,
∴∠ACB=∠ABC=60°,
又∵BD=CD,∠BDC=120°,
∴∠BCD=∠CBD=30°,
∴∠MBD=∠DCE=90°,
在△BMD和△CED中
∵
,
∴△BMD≌△CED(SAS),
∴DE=DM,
在△MDN和△EDN中
∵
,
∴△MDN≌△EDN(SAS),
∴MN=NE=NC-CE=NC-BM.
延长AC至E,使得CE=BM(或延长AB至E,使得BE=CN),并连接DE.
∵△BDC为等腰三角形,△ABC为等边三角形,
∴BD=CD,∠DBC=∠DCB,∠MBC=∠ACB=60°,
又BD=DC,且∠BDC=120°,
∴∠DBC=∠DCB=30°
∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°,
∴∠MBD=∠ECD=90°,
在△MBD与△ECD中,
∵
|
∴△MBD≌△ECD(SAS),
∴MD=DE,
∴△DMN≌△DEN,
∴MN=BM+NC.
(2)按要求作出图形,(1)中结论不成立,应为MN=NC-BM.
在CA上截取CE=BM.
∵△ABC是正三角形,
∴∠ACB=∠ABC=60°,
又∵BD=CD,∠BDC=120°,
∴∠BCD=∠CBD=30°,

∴∠MBD=∠DCE=90°,
在△BMD和△CED中
∵
|
∴△BMD≌△CED(SAS),
∴DE=DM,
在△MDN和△EDN中
∵
|
∴△MDN≌△EDN(SAS),
∴MN=NE=NC-CE=NC-BM.
点评:此题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质;此题从不同角度考查了作相等线段构造全等三角形的能力,要充分利用等边三角形及等腰三角形的性质,转换各相等线段解答.

练习册系列答案
相关题目



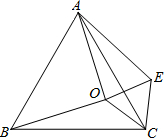 如图,点O是正△ABC内一点,∠AOB=90°,∠BOC=α,将△BOC绕点C顺时针旋转60°得到△AEC,连接OE
如图,点O是正△ABC内一点,∠AOB=90°,∠BOC=α,将△BOC绕点C顺时针旋转60°得到△AEC,连接OE