题目内容
【题目】如图，四边形是正方形
，
是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60度得到BN，连接
（1）求证：
（2）①当M点在何处时， 
的值最小；
②当M点在何处时，
的值最小，并说明理由
【答案】（1）见解析；（2）①当M点在BD的中点处时，A，M，C三点共线，
最小；②当M位于BD与CE交点处时，
的值最小，见解析
【解析】
（1）根据旋转的性质得BM=BN，∠MBN=60°，则可判断△ABE是等边三角形，得到BA=BE，∠ABE=60°，易得∠ABM=∠EBN，然后根据“SAS”可判断△AMB≌△ENB；（2）①连接AC，AC与BD相交于点O，如图1，根据正方形的性质得点O为BD的中点，根据两点之间线段最短得到AM+CM≥AC（当M点在AC上时取等号），于是得到当M点在BD的中点时，AM+CM的值最小；②由△BMN为等边三角形得BM=MN，由△AMB≌△ENB得EN=AM，根据两点之间线段最短，当点E、N、M、C共线时，AM+BM+CM的值最小．
（1）证明：
是等边三角形，
，
，
，
，
在
中，
，
；
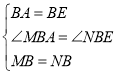（2）①如图，连接AC，AC与BD相交于点O，
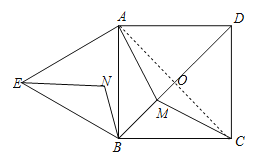
∵四边形ABCD是正方形，
∴点O为BD的中点，
∵AM+CM≥AC（当M点在AC上时取等号），
∴当M点在BD的中点时，AM+CM的值最小；
②如图，连接CE，当M位于BD与CE交点处时，的值最小；
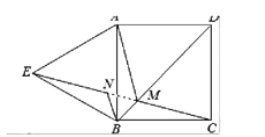
理由如下：连接由MN（1）知，，
，
，
是等边三角形，
，
，
根据两点之间线段最短知：若E，N，M，C在同一直线上时，
取得最小值，最小值为
，
在
中
，
，
，
，
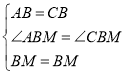若连接EC，则
，
，
可以同时在直线EC上．
所以当M点位于BD与CE的交点处时，的值最小，即等于EC的长．
练习册系列答案
阅读快车系列答案
相关题目
