题目内容
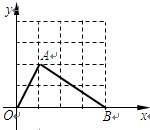
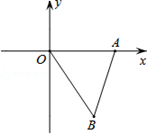
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ),点C的坐标为(
),点C的坐标为(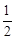 ,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
 ),点C的坐标为(
),点C的坐标为(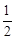 ,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
,0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
A.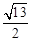 | B.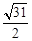 |
C.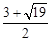 | D.2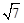 |
B.
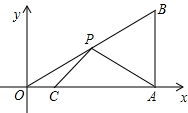
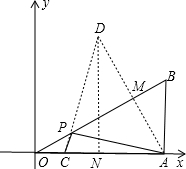
试题分析:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案:
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小.
∵DP=PA,∴PA+PC=PD+PC=CD.
∵B(3,
 ),∴AB=
),∴AB= ,OA=3,∠B=60°.
,OA=3,∠B=60°.由勾股定理得:OB=2
 .
.由三角形面积公式得:
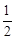 ×OA×AB=
×OA×AB=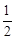 ×OB×AM,∴AM=
×OB×AM,∴AM=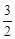 .∴AD=2×
.∴AD=2×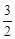 =3.
=3.∵∠AMB=90°,∠B=60°,∴∠BAM=30°.
∵∠BAO=90°,∴∠OAM=60°.
∵DN⊥OA,∴∠NDA=30°.∴AN=
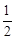 AD=
AD=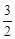 .
.由勾股定理得:DN=
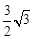 .
.∵C(
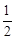 ,0),∴
,0),∴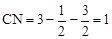 .
.在Rt△DNC中,由勾股定理得:
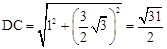 .
.∴PA+PC的最小值是
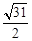 .
.故选B.
考点: 1.轴对称(最短路线问题);2.坐标与图形性质;3.勾股定理;4.含30度角直角三角形的性质.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目

 轴对称,并写出B1的坐标;(4分)
轴对称,并写出B1的坐标;(4分)


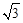 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为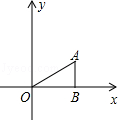
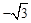 )
)