题目内容
如图所示，已知P是△ABC内一点，试说明PA+PB+PC＞
（AB+BC+AC）．
证明：在△ABP中：AP+BP＞AB．
同理：BP+PC＞BC，AP+PC＞AC．
以上三式分别相加得到：
2（PA+PB+PC）＞AB+BC+AC，
即PA+PB+PC＞（AB+BC+AC）．
分析：根据三角形的三边关系就可以证出．
点评：解本题的本题的关键是多次运用了三角形的三边关系定理．
同理：BP+PC＞BC，AP+PC＞AC．
以上三式分别相加得到：
2（PA+PB+PC）＞AB+BC+AC，
即PA+PB+PC＞
（AB+BC+AC）．分析：根据三角形的三边关系就可以证出．
点评：解本题的本题的关键是多次运用了三角形的三边关系定理．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
22、如图所示，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1m/s，点Q运动的速度是2m/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t s，解答下列问题：
19、如图所示，已知O是四边形ABCD内一点，OB=OC=OD，∠BCD=∠BAD=75°，则∠ADO+∠ABO=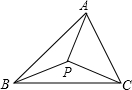
如图所示，已知P是△ABC内一点，试说明PA+PB+PC＞
如图所示，已知AB是半圆O的直径，弦CD∥AB，AB=10，CD=6，E是AB延长线上一点，BE=
20、如图所示，已知AB是半圆O的直径，∠BAC=22°，则∠B=